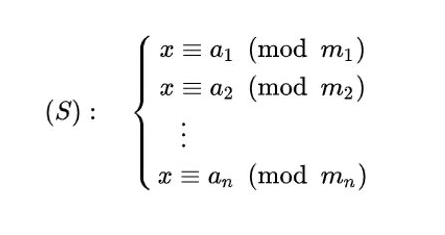数论基础知识

1.模运算

定义：

  $a$ 模 $n$ 的运算给出了 $a$ 对模 $n$ 的余数，这种运算称为模运算。注意：模运算的结果是从 0 到 $n-1$ 的一个整数。

  模运算就像普通的运算一样，它是可交换、可结合、可分配的。而且，对每一个中间结果进行模 $m$ 运算后再进行模 $m$ 运算，其作用与先进行全部运算，然后再进行模 $m$ 运算所得到的结果是一样的。例如：

$$(a+b)modm=((amodm)+(bmodm))modm$$$$(a-b)modm=((amodm)-(bmodm))modm$$$$(a\times b)modm=((amodm)\times (bmodm))modm$$$$(a\times (b+c))modm=((a\times b)modm+(a\times c)modm)modm$$

这些性质对于密码学中的数学计算非常的重要，模运算可以将所有中间结果和最后结果限制在一个范围内。对于一个 $k$ 位的模数 $n$ ，任何、加、减、乘的中间结果将不会超过 $2k$ 位长，这样避免了巨大的中间结果，使得计算机能够有效的处理数据。

如：计算 $a^8$(mod n)，不要直接进行 7 次乘法和一个大数的模运算：

$$(a\times a\times a\times a\times a\times a\times a\times a)modn$$

相反，应该进行三次比较小的乘法和三次比较小的模化简：

(($a^2$ mod n)${}^2$ mod n)${}^2$ mod n

这样就可以避免巨大的中间结果出现，这在实战中我们使用的是快速幂算法。

print(2**1000000000000000000 % 24)
print(pow(2,1000000000000000000,24))

2.欧拉函数

定义：

对正整数 $n$，欧拉函数是小于或等于 $n$ 的数中与 $n$ 互质的数的个数，

记作：$\phi (n)$

例如：$\phi (8)=4$ ,因为 $1，3，5，7$ 均与 $8$ 互质。

性质：

(1) 若 $n$ 为一素数 P，则：$\phi (P)=P-1$

(2) 如果 P 是素数，$k\ge 1$ ,则：$\phi (P^k)$ = $(P-1)\times P^{k-1}$

例如 ：求 φ(16)，由于 16 = 2×2×2×2，故 φ(16) = (2-1) ×$2^3$ = 8

(3) 若 n 为任意两个互质的 数 $a,b$ 的积，则：φ(a*b) = φ(a) × φ(b)

例：求 φ(40)，由于 40 = 5×8，所以 φ(40) = φ(5) × φ(8) = 4×4 = 16

(4)对于整数 $n\ge 2$，根据算术基本定理，$n$ 可以分解成唯一的形如 $n=p_1^{e_1}$$p_2^{e_2}$ ⋯$p_k^{e_k}$ 的分解式，则：$\phi (n)=n(1-\frac{1}{p_1})(1-\frac{1}{p_2})\cdots (1-\frac{1}{p_k})$

3.欧几里得(Euclid)算法

定义：

  欧几里得算法又称为辗转相除法，用于求两个数的最大公约数。

原理：$GCD(x,y)$ = $GCD$($y$，$x$ $mod$ $y$) ，$x>y$

1.python 代码实现

def GCD(x,y):
    if(y==0):
        return x
    else:
        return GCD(y,x%y)

2.python 第三方库：

gmpy2.gcd(a,b)     #求 a,b 的最大公约数

from gmpy2 import*
m = gcd(a,b)  #求a,b的最大公约数

Crypto.Util.number

from Crypto.Util.number import*
m = GCD(a,b)  #求a,b的最大公约数

4.扩展欧几里得算法

定义：

  在已知 $x，y$ 时，求解一组解 $a,b$，使得 $ax+by=GCD(x，y)$

算法输入：两个正整数 $x$ 和 $y$

算法输出：$x$ 和 $y$ 的最大公因数 $gcd(x,y)$ 及满足等式 $ax+by=gcd(x,y)$ 的整数 $a$ 和 $b$

python 代码实现:

gmpy2 库函数 gcdext()

from gmpy2 import*
x = 17
y = 65537

#扩展欧几里得算法
s = gcdext(x,y)

# 返回元祖tuple ，满足s[1]*x+s[2]*y = 1
print(s)
#输出：(mpz(1),mpz(30841),mpz(-8))
print(s[1]*x+s[2]*y)
# 输出:1

5.同余

定义：

  设 a,b 是整数，$n\ne 0$，如果 $n|(a-b)$，则称 $a$ 和 $b$ 模 $n$ 同余，记为 $a\equiv b$($mod$ $n$)，整数 $n$ 称为模数。

  由于 $n|(a-b)$ 等价于 $-n|(a-b)$，所以 $a\equiv b$($mod$ $n$) 与 $a\equiv b$ $($ $mod$ $(-n)$ $)$ 等价。因此，一般我们总假定模数 $n\ge 1$。

同余的性质

性质 1：

(1)自反性：a ≡ a (mod m)

(2)对称性：a ≡ b (mod m)， b ≡ c (mod m) ，则 a ≡ c (mod m)

性质 2：

(1) 若 $a\equiv b$ ($mod$ $m$)，$c\equiv d$ ($mod$ $m$)

则：$a\pm c\equiv b\pm d$ ($mod$ $m$)，$ac\equiv bd$ ($mod$ $m$)

特别的，对于一个整数 e,都有 $a\pm e\equiv b\pm e$ ($mod$ $m$)，$ae\equiv be$ ($mod$ $m$)

(2) 若 $a\equiv b$ ($mod$ $m$)，k>0，则 $ak\equiv bk$ $(mod$ $mk)$

(3) 若 $a\equiv b$ ($mod$ $m$)，d 是 a，b 的公因数，则 $\frac{a}{d}\equiv \frac{b}{d}$ (mod $\frac{m}{d}$)

(4) 若 $a\equiv b$ ($mod$ $m$)，d|m，d>0，则: a ≡ b (mod d)

(5) 若 $a\equiv b$ ($mod$ $m$)，则: $a^n$≡$b^n$ (mod m)

(6) $(a\times b)$ $mod$ $m$ = ($a$ $mod$ $m\times b$ $mod$ $m$ ) $mod$ $m$

(7) $a^b$ $mod$ $m$ = ($a$ $mod$ $m$)${}^b$ $mod$ $m$

6.逆运算

定义：

若 m≥1，$gcd(a,m)=1$,则存在 c 使得：

$$ca\equiv 1(modm)$$

我们把 c 称为 a 对模 n 的逆，记作 $a^{-1}$ (mod m)，在模数已经指明的情况下，有时也记作 $a^{-1}$。

在(a,m)=1 时，我们可以使用扩展欧几里得算法来求 a 的逆元：$a^{-1}$，这是因为：扩展欧几里得算法可以找到整数 $x$,$y$ 使得 $ax+my=1$，这样 $a^{-1}=x$ ($mod$ $n$)

7.中国剩余定理

中国剩余定理（Chinese remainder theorem，CRT），又称孙子定理，最早可见于中国南北朝时期（公元 5 世纪）的数学著作《孙子算经》中，为一次同余方程组的起源。

定理(CRT):

  设 $m_1,m_2,\cdots ,m_k$ 是两两互素的正整数，$M=m_1{m}_2\cdots m_k,$

$M_i=\frac{M}{m_i}(i=1,2,\cdots ,k)$,则同余方程组：

CRT|445

有唯一解: $x=a_1{M}_1{M}_1^{-1}+a_2{M}_2{M}_2^{-1}+\cdots +a_k{M}_k{M}_k^{-1}$ ($mod$ $M$)

其中 $M_i{M}_i^{-1}\equiv 1$ ($mod$ $m_i$)，i=1,2,⋯,k

代码实现：

from gmpy2 import*
from Crypto.Util.number import*
from functools import reduce

N1 = 
N2 = 
N3 = 
c1 =
c2 =
c3 =
e=3

n = [N1,N2,N3]
c = [c1,c2,c3]

def CRT(a,n):
    sum = 0
    N = reduce(lambda x,y:x*y,n)

    for n_i, a_i in zip(n,a):
        N_i = N // n_i
        sum += a_i*N_i*invert(N_i,n_i)
    return sum % N 

x = CRT(c,n)
m = iroot(x,e)[0]
print(long_to_bytes(m))

8.一般同余组

讨论一般同余组的情况，

**定理： ** 当 $m_1,m_2,\cdots ,m_k$ 是两两互素的正整数，则同余式 $a\equiv b(mod{m}_1{m}_2...m_k)$ 等价于同余式组

$$\{\begin{array}{l}a\equiv b(mod{m}_1)\\ a\equiv b(mod{m}_2)\\ ...\\ a\equiv b(mod{m}_k)\end{array}$$

反之也成立。

例题，有同余式组如下：

$$\{\begin{array}{l}x\equiv 3mod8\\ x\equiv 11mod20\\ x\equiv 1mod15\end{array}$$

点击查看答案

将上面同余式组化为如下形式：（这里的等于号全部代表同余号） x = 3 mod 8 x = 11 mod 4 = 3 mod 4 x = 11 mod 5 = 1 mod 5 x = 1 mod 3 x = 1 mod 5 满足第一个同余式，必满足第二个同余式，现在得到一个与原同余式等价并且可以利用中国剩余定量求解的同余式组： x = 3 mod 8 x = 1 mod 3 x = 1 mod 5 然后利用中国剩余定理即可求解。

9.费马小定理

若 a 为正整数，P 是一质数，则：gcd(a,p)=1，那么 $a^{p-1}$ ≡ $1(modp)$

$a^p$≡$a$ $mod$ $p$，推论: $a^p$ $mod$ $p$=$a$ $mod$ $p$

10.威尔逊定理

若 p 为素数，则：$(p-1)!\equiv -1$ $mod$ $p$ ⟹ 推导：$(p-2)!\equiv 1$ $mod$ $p$;

其逆定理同样成立。即：若 $(p-1)!\equiv -1$ $mod$ $p$ ，则 p 为素数

11.欧拉定理

若 a 与 m 互质，则：$a^{\phi (m)}\equiv 1modm$

12.二次剩余

一般模 N 的二次同余方程是最常见的同余方程，其中 $N=p\ast q$ 或 $N=p$ 的情况，这类同余方程的解一般归结于求二次剩余问题。下面我们讨论模为素数 p 的二次同余方程。

定义1： 设素数 $p>2,(p,a)=1$ 。如果二次同余式 $x^2\equiv amodp$ 有解，则称 a 是模 p 的 二次剩余；若无解，则称 a 是模 p 的二次非剩余。（又可称为平方剩余和平方非剩余）

记模 p 的二次剩余与二次非剩余的全体分别为：

$Q{R}_p=\{a|a\in Z_p^{\ast },\mathrm{存}\mathrm{在}x\in Z_p^{\ast },x^2\equiv amodp\}$

$QN{R}_p=\{a|a\in Z_p^{\ast },\mathrm{任}\mathrm{意}x\in Z_p^{\ast },x^2\ne amodp\}$

定义2： 在模 p 的既约剩余系中，二次剩余和二次非剩余各占一半，即：$|Q{R}_p|=|QN{R}_p|=\frac{p-1}{2}$

定理3(欧拉判别法)： 设素数 $p>2,(p,a)=1$，

那么 a 为模 p 的二次剩余的充要条件是：$a^{(p-1)/2}\equiv 1modp$

那么 a 为模 p 的二次非剩余的充要条件是：$a^{(p-1)/2}\equiv -1modp$

由定理3 得到的推论：

若 $p\equiv 1mod4$ ，则 $-1$ 是模 $p$ 的二次剩余

$p\equiv 3mod4$，则 $-1$ 是模 $p$ 的二次非剩余

如果 a 为模 p 的二次剩余，当 $p\equiv 3mod4$时，$\pm a^{(p+1)/4}$ 为同余方程 $x^2\equiv amodp$ 的解。

证明：因为a 为模 p 的二次剩余，所以 $a^{(p-1)/2}\equiv 1modp$，得到：

$(\pm a^{(p+1)/4}{)}^2=a^{(p-1)/2}\times a\equiv amodp$

求解二次剩余 $x^2\equiv amodp$ 的 $x$ 值，可以使用下列常见函数：

from sympy import legendre_symbol, sqrt_mod

legendre_symbol(a, p) # 计算 a 对模 p 的勒让德符号 
sqrt_mod(a, p) # 计算 a 的模 p 下的平方根

在 SageMath 中，可以使用 sqrt_mod() 函数来计算开模平方根。

sageCopy code
sqrt_mod(a, p)  # 计算 a 的模 p 下的平方根

13.勒让德符号

利用勒让德符号在判别是否二次剩余时非常有效。

定义： 设素数 $p>2$ ，a 是整数。令：

$$(\frac{a}{p})=\{\begin{array}{rcl}1,& & a\mathrm{是}\mathrm{模}p\mathrm{的}\mathrm{二}\mathrm{次}\mathrm{剩}\mathrm{余}\\ -1,& & a\mathrm{是}\mathrm{模}p\mathrm{的}\mathrm{二}\mathrm{次}\mathrm{非}\mathrm{剩}\mathrm{余}\\ 0,& & a\mathrm{能}\mathrm{够}\mathrm{被}p\mathrm{整}\mathrm{除}，\mathrm{即}p|a\end{array}$$

称 $(\frac{a}{p})$为模 p 的 Legenare 符号。

**定理1：**Legenare 符号的性质

（1）$(\frac{a}{p})\equiv a^{(p-1)/2}modp$

（2）$(\frac{1}{p})=1$ , $(\frac{-1}{p})=(-1{)}^{(p-1)/2}$

（3）如果 $a\equiv bmodp$， 则 $(\frac{a}{p})=\frac{b}{p}$

（4）$(\frac{a}{p})\equiv (\frac{a+p}{p})$

（5）$(\frac{ab}{p})\equiv (\frac{a}{p})(\frac{b}{p})$

（4）如果 $(a,p)=1$ ，则 $(\frac{a^2}{p})=1$

定理2：$(\frac{2}{p})=(-1{)}^{(p^2-1)/8}$

**定理3（Gauss 二次互反律）：**设 p,q 均为奇素数，$p\ne q$,那么有：$(\frac{q}{p})=(-1{)}^{(p-1)/2\ast (q-1)/2}(\frac{p}{q})$

14.雅可比符号

**定义：**设 $m$ 是大于1的奇数，$m=p_1{p}_2...p_r$ 是m的素数分解，$a$ 是整数。雅可比符号 $(\frac{a}{m})$ 定义如下：

$(\frac{a}{m})=(\frac{a}{p_1})(\frac{a}{p_2})...(\frac{a}{p_r})$ 其中 $(\frac{a}{p_i})$ 是勒让德符号。

注：雅可比符号并不能判断 $a$ 是否是模 $m$ 的平方剩余。

有如下性质：

（1）$(\frac{1}{m})=1$

（2）$(a,m)=1\mathrm{时}，(\frac{a^2}{m})=1$

（3）如果 $a\equiv bmodm$ ，则 $(\frac{a}{m})=(\frac{b}{m})$

（4）$(\frac{a}{m})=(\frac{a+m}{m})$

（5）$(\frac{ab}{m})=(\frac{a}{m})(\frac{b}{m})$

（6）$(\frac{-1}{m})=(-1{)}^{\frac{m-1}{2}}$

（7）$(\frac{2}{m})=(-1{)}^{\frac{m^2-1}{8}}$

15.指数与原根

原根的概念类似于循环群的生成元和有限域中的本原元。

**定义：**设m是大于1的正整数，如果 (a,m) = 1，则使同余式 $a^d\equiv 1modm$ 成立的最小正整数 $d$ 称为 $a$ 对模 $m$ 的指数（或阶），记为$or{d}_m(a)$。

如果 $a$ 对模 $m$ 的指数是 $\phi (m)$ ，则 $a$ 称为模 $m$ 的一个原根。

**指数的性质：**下列的性质中，都假设$(a,m)=1$ ，$a$ 对模 $m$ 的阶为 $or{d}_m(a)$

1、如果 $a\equiv bmodm$ ，则 $or{d}_m(a)=or{d}_m(b)$

2、设 $a^{-1}$ 是 $a$ 模 $m$ 的逆元，即 $a^{-1}a\equiv 1modm$ ，则 $or{d}_m(a^{-1})=or{d}_m(a)$

3、 $a^d\equiv a^{k}modm$ ，则 $d\equiv kmodor{d}_m(a)$

原根的存在性：

定理1：对于如果p是奇素数，则存在模 p 的原根

定理2：设 $\phi (m)$ 的不同素因子为：$q_1,q_2,...,q_k$ ，则 $g((g,m)=1)$ 是模m的一个原根的充要条件是 ：$g^{\frac{\phi (m)}{q_i}}\ne 1(modm),i=1,2,..,k$

16.离散对数

定义：设 $g$ 是模$m$的一个原根，对于任一整数$a，(a,m)=1$，都有 $a\equiv g^r(modm)，0<=r<=\phi (m)$，把 $r$称为以$g$为底的 $a$ 对模 $m$ 的离散对数，记为 $in{d}_{g}a$ 。离散对数也称为指标。

离散对数在密码学中具有非常重要的意义，当给定 $m,g,in{d}_{g}a$ 时，存在有效的算法计算出 $a\equiv g^{in{d}_{g}a}(modm)$ 。但给定 $m,g,a$ 时，在特定的条件下，比如 $m$ 是一个大素数时，计算 $in{d}_{g}a$ 会非常困难。这样的离散对数难题是构造公钥密码学体制的重要基础之一。

17.椭圆曲线

离散对数困难问题可以分为有限域上的离散对数困难问题和椭圆曲线上的离散对数困难问题。

椭圆曲线 $E$ 是由标准形式的三次曲线： $y^2+a_{1}xy+a_{3}y=x^3+a_2{x}^2+a_{4}x+a_6$ (系数 $a_i$ 属于域 $K$) 的所有解$(x,y)\in K$ 的集合，以及一个无穷远点 $O$ 组成的。

对于一般的数域 $K$ ，椭圆曲线可以化简成如下形式表示：$y^2=x^3+ax+b$

定义1： 设 $E$ 是域 $K$ 上的椭圆曲线，$P、Q$ 是椭圆曲线 $E$ 任意的两个点，定义加法“+” 算法如下：

（1）$P+O=P,O+P=P$ (单位元为无穷远点$O$)

（2）$-O=O$

（3）如果 $P=(x_1,y_1)\ne O$，那么 $-P=(x_1,-y_1-a_1{x}_1-a_3)$

（4）如果 $Q=-P$，则 $P+Q=O$

（5）如果 $P\ne O，Q\ne O，P\ne -Q$，那么

1、如果 $P\ne Q$，则 $R$ 是直线 $PQ$ （经过点$P$和点$Q$的直线）与椭圆曲线相交的第三个点。

2、如果 $P=Q$，则 $R$ 是椭圆曲线在点$P$的切线与椭圆曲线相交的另一个点，因此 $P+Q=-R$ 。

定义2： 在椭圆曲线 $E$ 上定义加法运算 “$+$ ” ，设 $P(x_1,y_1),Q(x_2,y_2)\in E$，$O$ 是椭圆曲线上的无穷远点，则

（1）$P+O=P$ （$O$为无穷远点）；

（2）若 $x_1=x_2,y_1=-y_2$，则 $P+Q=O$ ；

（3）当 $P+Q=(x_3,y_3)$ ，其中

$$\{\begin{array}{l}{x}_3={\lambda }^2-x_1-x_2\\ y_3=\lambda (x_1-x_3)-y_1\end{array}$$$$\lambda =\{\begin{array}{ll}\frac{y_2-y_1}{x_2-x_1},& \mathrm{如}\mathrm{果}P\ne Q\\ \frac{3x_1^2+a}{2y_1},& \mathrm{如}\mathrm{果}P=Q\end{array}$$

如果 $P+Q=O$,则记 $Q=-P$ ，并称 $-P$ 为 $P$ 的逆元。

一般地，我们将 $\underset{n\mathrm{次}}{\underbrace{P+P+\cdot \cdot \cdot +P}}$ 记为 $nP$ ，即 $np=$ $\underset{n\mathrm{次}}{\underbrace{P+P+\cdot \cdot \cdot +P}}$，同时，定义：$nP=O$（单位元）

以上定义的加法运算具有鲜明的几何意义:

（1）若 $x_1=x_2,y_1=-y_2$，此时它们的连线与 $x$ 轴垂直相交，并与椭圆曲线交于无穷远点 $O$，所以 $P+Q=O$

（2）如果 $x_1\ne x_2$，则 $R(x_3,y_3)$ 是直线 $PQ$ （经过点$P$和点$Q$的直线）与椭圆曲线相交的第三个点，那么 $P+Q+R=O$；

（3）若求 $2P$，只需要画出 $P$ 点的切线，该切线与椭圆曲线的另一个交点 $R$ 满足 $P+P+R=O$，则 $R$ 关于x轴的对称点即所求的 $2P$ 。

18.群的定义

群 G (group) 是满足四大标准性质的任意集合，含有一个二元运算 ∗ ；

群的性质：

1）封闭性：群在运算 $\ast$ 下是封闭的，对于群中的任意两个元素 a 和 b，a∗b 也是 G 中的一个元素；

2）有单位元：群 G 中含有单位元 e ，对于群 G 中的每个元素 a 都满足 $a\ast e=e\ast a$ ；

3）存在逆元：群 G 中的每个元素 a 都存在逆元(inverse)，记作 $a^{-1}$ ，满足性质 $a\ast a^{-1}=a^{-1}\ast a=e$

4）结合律：$(a\ast b)\ast c=a\ast (b\ast c)$

当群中的运算用于将一个元素与其自身相运算多次的时候，可以采用指数运算来表示：$k$ 个 $a\ast a\ast \cdots \ast a$ = $a^k$

有限群群 G 中所含元素的个数称为群的阶，记作 order(G)。

19.曲线阶的性质

定义曲线的阶为 $r=E.order()$

对于椭圆曲线 $E$ 上的任意一点 $P$ ，有：$r\ast P=0(\mathrm{无}\mathrm{穷}\mathrm{远}\mathrm{点})$

ECC 中的点乘和逆运算：

假设 $P=e\ast G$ ，我们希望求解 $G$ ，如果我们能找到 $e$ 的模 $r$ 逆元 $e^{-1}$ ，即满足 $e\ast e^{-1}\equiv 1modr$ ，那么可以进行如下计算：

• $P=e\ast G$
• $e^{-1}\ast P=e^{-1}\ast e\ast G$
• $e^{-1}\ast P=(1+k\ast r)\ast G=G+k\ast r\ast G=G$ (其中 r*G = 0)

群的性质：在椭圆曲线上，所有的点（包括无穷远点O）构成了一个循环群。群的阶 $r$ 是指该群中元素的数量。对于任何属于该群的点 $G$ ，都有 $r\ast G=O$ 。这意味着当我们对 $G$ 进行 $r$ 次倍乘时，结果将是无穷远点。因此，在求 $e$ 的逆元时，我们是在模 $r$ 的条件下寻找 $e$ 的逆元。

样例：

from sage.all import *
from Crypto.Util.number import *
from gmpy2 import *

p = getPrime(220)
a = getPrime(20)
b = getPrime(20)
E = EllipticCurve(GF(p),[a,b])
G = E.random_point()
r = E.order()
print(r*G)

输出：

(0 : 1 : 0)

一个比较好的文章：https://suntus.github.io/2019/05/31/ECC算法/