私钥 d 相关攻击

N1Key2023/5/7大约 22 分钟维纳攻击及变种Pell方程构造不安全的私钥d已知d分解N

已知 d 分解 N

已知 (n,e,d) 求 p,q

实现算法：https://www.di-mgt.com.au/rsa_factorize_n.html

def getpq(n, e, d):
    """
    Factorize n using d as a hint.
    Returns: a tuple (p, q) such that p*q = n.
    Algorithm: <https://www.di-mgt.com.au/rsa_factorize_n.html>
    """
    p = 1
    q = 1
    while p == 1 and q == 1:
        k = d * e - 1
        g = random.randint(0, n)
        while p == 1 and q == 1 and k % 2 == 0:
            k = k // 2
            x = pow(g, k, n)
            if x != 1 and gcd(x - 1, n) > 1:
                p = gcd(x - 1, n)
                q = n // p
    return p, q

连分数方法攻击 RSA

背景：为了提高RSA的解密速度，一种有效的方法就是选取较小的解密指数 d 。例如智能卡与大型服务器之间的通信，由于智能卡本身的计算能力有限，所以智能卡通常选取较小的解密指数 d ，而大型服务器则使用较大的加密指数 e 。由 Wiener 首次提出利用连分数可以攻击小解密指数的 RSA ，即当 $d < \frac{1}{3} N^{0.25}$ ，可以分解 RSA 的模 N

参考学习 Blog:
Lazzaro ， Van1sh

学习连分数的一个网址： https://chaoli.club/index.php/2756

连分数定义

简单连分数形式如下：

$a_{1} + \frac{1}{a_{2} + \frac{1}{a_{3} + \frac{1}{a_{4} + . . .}}}$

其中 $a_{1}$ 是整数， $a_{2} ， a_{3} ， a_{4} ， . . .$ 是正整数。如果项数有限，则称为有限简单连分数；否则，称为无限简单连分数。用符号 $[a_{1}, a_{2}, . . ., a_{k}, . . .]$ 来表示简单连分数

定理 I：

如果 $\frac{p_{1}}{q_{1}}, \frac{p_{2}}{q_{2}}, . . ., \frac{p_{3}}{q_{3}}, . . .$ 是简单连分数 $[a_{1}, a_{2}, . . ., a_{k}, . . .]$ 的渐进分数，则有如下递推公式：

$p_{1} = a_{1} ， p_{2} = a_{2} a_{1} + 1 ， p_{k} = a_{k} p_{k - 1} + p_{k - 2}$

$q_{1} = 1 ， q_{2} = a_{2} ， q_{k} = a_{k} q_{k - 1} + q_{k - 2} ， (k \geq 3)$

定理 II：

若 $α$ 是任一实数，有理数 $\frac{p}{q}$ 满足 $| α - \frac{p}{q} | < \frac{1}{2 q^{2}}$ ，则 $\frac{p}{q}$ 必为 $α$ 的某一渐进分数

Wiener攻击变种 1

Attack on Prime Power RSA with Two RSA Moduli
Paper: https://eprint.iacr.org/2015/399.pdf

通过对 $\frac{N_{2}}{N_{1}}$ 进行连分数展开求其各项的渐进分数，记为 $\frac{t_{i}}{s_{i}}$ 并验证 $N_{2}$ % $t_{k} == 0$ 是否成立；如果成立，则： $q_{2} = t_{k}, q_{1} = s_{k}$

EXP：

from Crypto.Util.number import long_to_bytes
from gmpy2 import *


def transform(x, y):  # 使用辗转相除法将分数 x/y 转为连分数的形式
    res = []
    while y:
        res.append(x // y)
        x, y = y, x % y
    return res


def continued_fraction(sub_res):
    numerator, denominator = 1, 0
    for i in sub_res[::-1]:  # 从sublist的后面往前循环
        denominator, numerator = numerator, i * numerator + denominator
    return numerator, denominator  # 得到渐进分数的分母和分子，并返回

    # 求解每个渐进分数


def sub_fraction(x, y):
    res = transform(x, y)
    res = list(map(continued_fraction, (res[0:i] for i in range(1, len(res) + 1))))  # 将连分数的结果逐一截取以求渐进分数
    return res


def wienerAttack(n2, n1):
    for (q2, q1) in sub_fraction(n2, n1):  # 用一个for循环来注意试探 n2/n1 的连续函数的渐进分数，直到找到一个满足条件的渐进分数
        if q2 == 0:  # 可能出现连分数第一个值为0的情况，排除
            continue
        if n2 % q2 == 0 and q2 != 1:
            return (q2, q1)
    print("该方法不适用")


N1=60143104944034567859993561862949071559877219267755259679749062284763163484947626697494729046430386559610613113754453726683312513915610558734802079868190554644983911078936369464590301246394586190666760362763580192139772729890492729488892169933099057105842090125200369295070365451134781912223048179092058016446222199742919885472867511334714233086339832790286482634562102936600597781342756061479024744312357407750731307860842457299116947352106025529309727703385914891200109853084742321655388368371397596144557614128458065859276522963419738435137978069417053712567764148183279165963454266011754149684758060746773409666706463583389316772088889398359242197165140562147489286818190852679930372669254697353483887004105934649944725189954685412228899457155711301864163839538810653626724347
c1=55094296873556883585060020895253176070835143350249581136609315815308788255684072804968957510292559743192424646169207794748893753882418256401223641287546922358162629295622258913168323493447075410872354874300793298956869374606043622559405978242734950156459436487837698668489891733875650048466360950142617732135781244969524095348835624828008115829566644654403962285001724209210887446203934276651265377137788183939798543755386888532680013170540716736656670269251318800501517579803401154996881233025210176293554542024052540093890387437964747460765498713092018160196637928204190194154199389276666685436565665236397481709703644555328705818892269499380797044554054118656321389474821224725533693520856047736578402581854165941599254178019515615183102894716647680969742744705218868455450832
E1=125932919717342481428108392434488550259190856475011752106073050593074410065655587870702051419898088541590032209854048032649625269856337901048406066968337289491951404384300466543616578679539808215698754491076340386697518948419895268049696498272031094236309803803729823608854215226233796069683774155739820423103

N2=60143104944034567859993561862949071559877219267755259679749062284763163484947626697494729046430386559610613113754453726683312513915610558734802079868195633647431732875392121458684331843306730889424418620069322578265236351407591029338519809538995249896905137642342435659572917714183543305243715664380787797562011006398730320980994747939791561885622949912698246701769321430325902912003041678774440704056597862093530981040696872522868921139041247362592257285423948870944137019745161211585845927019259709501237550818918272189606436413992759328318871765171844153527424347985462767028135376552302463861324408178183842139330244906606776359050482977256728910278687996106152971028878653123533559760167711270265171441623056873903669918694259043580017081671349232051870716493557434517579121
c2=39328446140156257571484184713861319722905864197556720730852773059147902283123252767651430278357950872626778348596897711320942449693270603776870301102881405303651558719085454281142395652056217241751656631812580544180434349840236919765433122389116860827593711593732385562328255759509355298662361508611531972386995239908513273236239858854586845849686865360780290350287139092143587037396801704351692736985955152935601987758859759421886670907735120137698039900161327397951758852875291442188850946273771733011504922325622240838288097946309825051094566685479503461938502373520983684296658971700922069426788236476575236189040102848418547634290214175167767431475003216056701094275899211419979340802711684989710130215926526387138538819531199810841475218142606691152928236362534181622201347
E2=125932919717342481428108392434488550259190856475011752106073050593074410065655587870702051419898088541590032209854048032649625269856337901048406066968337289491951404384300466543616578679539808215698754491076340386697518948419895268049696498272031094236309803803729823608854215226233796069683774155739820425393

q2,q1 = wienerAttack(N2, N1)    #利用wiener攻击计算出 q1,q2的值
print("q2=", q2)
print("q1=", q1)

# q2= 11628371843051760370952910026406764366191062991235308941262037248377376991693250742343307155422036713746576338866595433599862614339347536916226536644211929
# q1= 11628371843051760370952910026406764366191062991235308941262037248377376991693250742343307155422036713746576338866595433599862614339347536916226536644210947
#常规RSA解密
p1 = iroot(N1//q1,2)[0]
p2 = iroot(N2//q2,2)[0]
phi1 = p1*(p1-1)*(q1-1)
phi2 = p2*(p2-1)*(q2-1)

d1 = invert(E1,phi1)
d2 = invert(E2,phi2)

m1 = pow(c1,d1,N1)
m2 = pow(c2,d2,N2)

print(long_to_bytes(m1)+long_to_bytes(m2))

Wiener攻击变种 2 （d > N^0.25）

Paper： A variant of Wiener’s attack on RSA （主要看这篇就行了）
CONTINUED FRACTIONS AND RSA WITH SMALL SECRET EXPONENT

1997年，Verheul 和 van Tilborg 提出了 Wiener 攻击的扩展，当 d 比 n^0.25 长几位时，可以破坏RSA密码系统。对于 $d > n^{0.25}$ 他们的攻击需要对大约 2t+8 bits 进行彻底搜索（在所涉及的部分收敛的合理假设下），其中 $t = l o g_{2} (d / n^{0.25})$

对于维纳攻击的扩展，其中 $d = r q_{m + 1} + s q_{m}$ ，对d的所有可能性进行测试，可能性的数量大致等于（r的可能性的数量）×（s的可能性的数目）

d 是 e/N 的连分数渐进分母， $q_{m + 1} 和 q_{m}$ 分别是 (e/N) 的连分数的第 (m+1) 个分母和第 m 个分母

勒让德定理的推广：

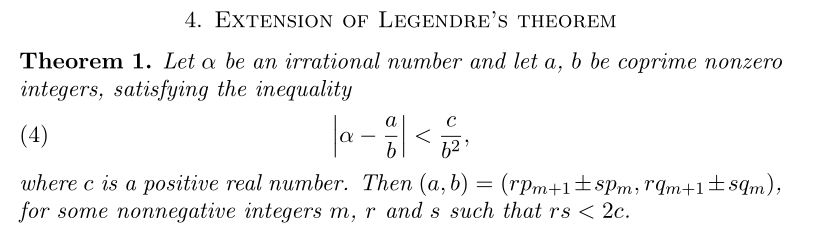
Wiener变种攻击的验证：

例题： ASIS Finals CTF 2017

from gmpy import *
from Crypto.Util.number import *
import gensafeprime    
from flag import FLAG

def make_pubpri(nbit):
    p, q, r = [ getPrime(nbit) for _ in xrange(3)]
    n = p * q * r
    phi = (p-1)*(q-1)*(r-1)
    l = min([p, q, r])
    d = getPrime(1 << 8)
    e = inverse(d, phi)
    a = gensafeprime.generate(2*nbit)
    while True:
        g = getRandomRange(2, a)
        if pow(g, 2, a) != 1 and pow(g, a/2, a) != 1:
            break
    return (n, e, a, g), (n, d, a, g)

def encrypt(m, pub):
    n, e, a, g = pub
    k = getRandomRange(2, a)
    K = pow(g, k, a)
    c1, c2 = pow(k, e, n), (m * K) % a
    return c1, c2

nbit = 512
pubkey, privkey = make_pubpri(nbit)
m = bytes_to_long(FLAG)
c = encrypt(m, pubkey)
print 'c =', c
print 'pubkey =', pubkey                                                                                                                                                                                                                          

c = (1569733526826523065259704222721381245770313117205865099913421859731162526943498524936251685846967970606251353344665893442015804015671457823645874503670136308040791285744658847419176471348768113798503897694020110157476679833746227801224812046930570487233225157924912272791212802495997329083436189937249314855532400635293522270501567950040825794060896420481676398789310029592608176167251882124182145471818654414925639589921023176070657483148482403065241178276749773L, 139537660044872985880471632333334179976891152860359271230202507995985566816703080930428310461057387079799847266510420206696052591677854190150642820963140050439023069266243433278700748622126726137374130247097863526461696642750021196138340072411724739383716017406022211953417323065831672315854246554523225039827L)
pubkey = (1696852658826990842058316561963467335977986730245296081842693913454799128341723605666024757923000936875008280288574503060506225324560725525210728761064310034604441130912702077320696660565727540525259413564999213382434231194132697630244074950529107794905761549606578049632101483460345878198682237227139704889943489709170676301481918176902970896183163611197618458670928730764124354693594769219086662173889094843054787693685403229558143793832013288487194871165461567L, 814161885590044357190593282132583612817366020133424034468187008267919006610450334193936389251944312061685926620628676079561886595567219325737685515818965422518820810326234612624290774570873983198113409686391355443155606621049101005048872030700143084978689888823664771959905075795440800042648923901406744546140059930315752131296763893979780940230041254506456283030727953969468933552050776243515721233426119581636614777596169466339421956338478341355508343072697451L, 171012227587318507773834753911094468358648971527111097308935888531930900156798659257578479378777764146070352809723708236353390208094909385240006920137781562826981091183813955039359863361624869703055918575613667858215532572602435432258750639197322091887713402631456113333645709142822182724397962837201266977523L, 96969753191136466007366303619618019752521508403657426306543836447071659732926802256183021740376016065813234292694535879838415771865207311953800116203362150588941093508091412441933752168889516206420588410478242229762908362637083786338280959547015086176046206126019992386890758970740552952647510652431386064722L)

EXP：

variant of wiener's attack 计算私钥 d 值

#sage
from sage.all import continued_fraction
def wiener(e,n):
    m = 12345
    c = pow(m,e,n)
    q0 = 1
    list = continued_fraction(e/n)   #计算连分数
    conv = list.convergents()    #计算渐近分数
    for i in conv:
        q1 = i.denominator()    #渐近分母

        for r in range(20):
            for s in range(20):
                d = r*q1 + s*q0
                m1 = pow(c,d,n)
                if m1 == m:
                    return d
        q0 = q1

c = (
    1569733526826523065259704222721381245770313117205865099913421859731162526943498524936251685846967970606251353344665893442015804015671457823645874503670136308040791285744658847419176471348768113798503897694020110157476679833746227801224812046930570487233225157924912272791212802495997329083436189937249314855532400635293522270501567950040825794060896420481676398789310029592608176167251882124182145471818654414925639589921023176070657483148482403065241178276749773,
    139537660044872985880471632333334179976891152860359271230202507995985566816703080930428310461057387079799847266510420206696052591677854190150642820963140050439023069266243433278700748622126726137374130247097863526461696642750021196138340072411724739383716017406022211953417323065831672315854246554523225039827
)
pubkey = (1696852658826990842058316561963467335977986730245296081842693913454799128341723605666024757923000936875008280288574503060506225324560725525210728761064310034604441130912702077320696660565727540525259413564999213382434231194132697630244074950529107794905761549606578049632101483460345878198682237227139704889943489709170676301481918176902970896183163611197618458670928730764124354693594769219086662173889094843054787693685403229558143793832013288487194871165461567,
          814161885590044357190593282132583612817366020133424034468187008267919006610450334193936389251944312061685926620628676079561886595567219325737685515818965422518820810326234612624290774570873983198113409686391355443155606621049101005048872030700143084978689888823664771959905075795440800042648923901406744546140059930315752131296763893979780940230041254506456283030727953969468933552050776243515721233426119581636614777596169466339421956338478341355508343072697451,
          171012227587318507773834753911094468358648971527111097308935888531930900156798659257578479378777764146070352809723708236353390208094909385240006920137781562826981091183813955039359863361624869703055918575613667858215532572602435432258750639197322091887713402631456113333645709142822182724397962837201266977523,
          96969753191136466007366303619618019752521508403657426306543836447071659732926802256183021740376016065813234292694535879838415771865207311953800116203362150588941093508091412441933752168889516206420588410478242229762908362637083786338280959547015086176046206126019992386890758970740552952647510652431386064722)
c1,c2 = c
n, e, a, g = pubkey

d = wiener(e,n)
# d=100556095937036905102538523179832446199526507742826168666218687736467897968451

剩下的常规RSA解密，中间有一步计算 c2 = (m*K) % a ，先计算出 K 值的逆元，再计算出 m

from gmpy2 import *
from libnum import *
k = pow(c1,d,n)
K = pow(g,k,a)
m = (c2*invert(mpz(K),mpz(a)))% a
print(n2s(int(m)))

Boneh-Durfee 攻击 (1/3 N^0.25<d<N0.292)

当公钥 e 指数值很大时，而私钥指数 $d$ 与模数 $N$ 相比太小，那么有效攻击为： $\frac{1}{3} N^{0.25} < d < N^{0.292}$

参考 https://github.com/mimoo/RSA-and-LLL-attacks
https://github.com/mimoo/RSA-and-LLL-attacks/blob/master/boneh_durfee.sage

实现 EXP:

from __future__ import print_function
import time

"""
Setting debug to true will display more informations
about the lattice, the bounds, the vectors...
"""
debug = True

"""
Setting strict to true will stop the algorithm (and
return (-1, -1)) if we don't have a correct
upperbound on the determinant. Note that this
doesn't necesseraly mean that no solutions
will be found since the theoretical upperbound is
usualy far away from actual results. That is why
you should probably use `strict = False`
"""
strict = False

"""
This is experimental, but has provided remarkable results
so far. It tries to reduce the lattice as much as it can
while keeping its efficiency. I see no reason not to use
this option, but if things don't work, you should try
disabling it
"""
helpful_only = True
dimension_min = 7  # stop removing if lattice reaches that dimension


############################################
# Functions
##########################################

# display stats on helpful vectors
def helpful_vectors(BB, modulus):
    nothelpful = 0
    for ii in range(BB.dimensions()[0]):
        if BB[ii, ii] >= modulus:
            nothelpful += 1

    print(nothelpful, "/", BB.dimensions()[0], " vectors are not helpful")


# display matrix picture with 0 and X
def matrix_overview(BB, bound):
    for ii in range(BB.dimensions()[0]):
        a = ('%02d ' % ii)
        for jj in range(BB.dimensions()[1]):
            a += '0' if BB[ii, jj] == 0 else 'X'
            if BB.dimensions()[0] < 60:
                a += ' '
        if BB[ii, ii] >= bound:
            a += '~'
        print(a)


# tries to remove unhelpful vectors
# we start at current = n-1 (last vector)
def remove_unhelpful(BB, monomials, bound, current):
    # end of our recursive function
    if current == -1 or BB.dimensions()[0] <= dimension_min:
        return BB

    # we start by checking from the end
    for ii in range(current, -1, -1):
        # if it is unhelpful:
        if BB[ii, ii] >= bound:
            affected_vectors = 0
            affected_vector_index = 0
            # let's check if it affects other vectors
            for jj in range(ii + 1, BB.dimensions()[0]):
                # if another vector is affected:
                # we increase the count
                if BB[jj, ii] != 0:
                    affected_vectors += 1
                    affected_vector_index = jj

            # level:0
            # if no other vectors end up affected
            # we remove it
            if affected_vectors == 0:
                print("* removing unhelpful vector", ii)
                BB = BB.delete_columns([ii])
                BB = BB.delete_rows([ii])
                monomials.pop(ii)
                BB = remove_unhelpful(BB, monomials, bound, ii - 1)
                return BB

            # level:1
            # if just one was affected we check
            # if it is affecting someone else
            elif affected_vectors == 1:
                affected_deeper = True
                for kk in range(affected_vector_index + 1, BB.dimensions()[0]):
                    # if it is affecting even one vector
                    # we give up on this one
                    if BB[kk, affected_vector_index] != 0:
                        affected_deeper = False
                # remove both it if no other vector was affected and
                # this helpful vector is not helpful enough
                # compared to our unhelpful one
                if affected_deeper and abs(bound - BB[affected_vector_index, affected_vector_index]) < abs(
                        bound - BB[ii, ii]):
                    print("* removing unhelpful vectors", ii, "and", affected_vector_index)
                    BB = BB.delete_columns([affected_vector_index, ii])
                    BB = BB.delete_rows([affected_vector_index, ii])
                    monomials.pop(affected_vector_index)
                    monomials.pop(ii)
                    BB = remove_unhelpful(BB, monomials, bound, ii - 1)
                    return BB
    # nothing happened
    return BB


""" 
Returns:
* 0,0   if it fails
* -1,-1 if `strict=true`, and determinant doesn't bound
* x0,y0 the solutions of `pol`
"""


def boneh_durfee(pol, modulus, mm, tt, XX, YY):
    """
    Boneh and Durfee revisited by Herrmann and May

    finds a solution if:
    * d < N^delta
    * |x| < e^delta
    * |y| < e^0.5
    whenever delta < 1 - sqrt(2)/2 ~ 0.292
    """

    # substitution (Herrman and May)
    PR.<u,x,y> = PolynomialRing(ZZ)
    Q = PR.quotient(x * y + 1 - u)  # u = xy + 1
    polZ = Q(pol).lift()

    UU = XX * YY + 1

    # x-shifts
    gg = []
    for kk in range(mm + 1):
        for ii in range(mm - kk + 1):
            xshift = x ^ ii * modulus ^ (mm - kk) * polZ(u, x, y) ^ kk
            gg.append(xshift)
    gg.sort()

    # x-shifts list of monomials
    monomials = []
    for polynomial in gg:
        for monomial in polynomial.monomials():
            if monomial not in monomials:
                monomials.append(monomial)
    monomials.sort()

    # y-shifts (selected by Herrman and May)
    for jj in range(1, tt + 1):
        for kk in range(floor(mm / tt) * jj, mm + 1):
            yshift = y ^ jj * polZ(u, x, y) ^ kk * modulus ^ (mm - kk)
            yshift = Q(yshift).lift()
            gg.append(yshift)  # substitution

    # y-shifts list of monomials
    for jj in range(1, tt + 1):
        for kk in range(floor(mm / tt) * jj, mm + 1):
            monomials.append(u ^ kk * y ^ jj)

    # construct lattice B
    nn = len(monomials)
    BB = Matrix(ZZ, nn)
    for ii in range(nn):
        BB[ii, 0] = gg[ii](0, 0, 0)
        for jj in range(1, ii + 1):
            if monomials[jj] in gg[ii].monomials():
                BB[ii, jj] = gg[ii].monomial_coefficient(monomials[jj]) * monomials[jj](UU, XX, YY)

    # Prototype to reduce the lattice
    if helpful_only:
        # automatically remove
        BB = remove_unhelpful(BB, monomials, modulus ^ mm, nn - 1)
        # reset dimension
        nn = BB.dimensions()[0]
        if nn == 0:
            print("failure")
            return 0, 0

    # check if vectors are helpful
    if debug:
        helpful_vectors(BB, modulus ^ mm)

    # check if determinant is correctly bounded
    det = BB.det()
    bound = modulus ^ (mm * nn)
    if det >= bound:
        print("We do not have det < bound. Solutions might not be found.")
        print("Try with highers m and t.")
        if debug:
            diff = (log(det) - log(bound)) / log(2)
            print("size det(L) - size e^(m*n) = ", floor(diff))
        if strict:
            return -1, -1
    else:
        print("det(L) < e^(m*n) (good! If a solution exists < N^delta, it will be found)")

    # display the lattice basis
    if debug:
        matrix_overview(BB, modulus ^ mm)

    # LLL
    if debug:
        print("optimizing basis of the lattice via LLL, this can take a long time")

    BB = BB.LLL()

    if debug:
        print("LLL is done!")

    # transform vector i & j -> polynomials 1 & 2
    if debug:
        print("looking for independent vectors in the lattice")
    found_polynomials = False

    for pol1_idx in range(nn - 1):
        for pol2_idx in range(pol1_idx + 1, nn):
            # for i and j, create the two polynomials
            PR.<w,z> = PolynomialRing(ZZ)
            pol1 = pol2 = 0
            for jj in range(nn):
                pol1 += monomials[jj](w * z + 1, w, z) * BB[pol1_idx, jj] / monomials[jj](UU, XX, YY)
                pol2 += monomials[jj](w * z + 1, w, z) * BB[pol2_idx, jj] / monomials[jj](UU, XX, YY)

            # resultant
            PR.<q> = PolynomialRing(ZZ)
            rr = pol1.resultant(pol2)

            # are these good polynomials?
            if rr.is_zero() or rr.monomials() == [1]:
                continue
            else:
                print("found them, using vectors", pol1_idx, "and", pol2_idx)
                found_polynomials = True
                break
        if found_polynomials:
            break

    if not found_polynomials:
        print("no independant vectors could be found. This should very rarely happen...")
        return 0, 0

    rr = rr(q, q)

    # solutions
    soly = rr.roots()

    if len(soly) == 0:
        print("Your prediction (delta) is too small")
        return 0, 0

    soly = soly[0][0]
    ss = pol1(q, soly)
    solx = ss.roots()[0][0]

    #
    return solx, soly


def example(N,e,delta,m):
    # you need to be a lattice master to tweak these
    t = int((1 - 2 * delta) * m)  # optimization from Herrmann and May
    X = 2 * floor(N ^ delta)  # this _might_ be too much
    Y = floor(N ^ (1 / 2))  # correct if p, q are ~ same size

    #
    # Don't touch anything below
    #

    # Problem put in equation
    P.<x,y> = PolynomialRing(ZZ)
    A = int((N + 1) / 2)
    pol = 1 + x * (A + y)

    #
    # Find the solutions!
    #

    # Checking bounds
    if debug:
        print("=== checking values ===")
        print("* delta:", delta)
        print("* delta < 0.292", delta < 0.292)
        print("* size of e:", int(log(e) / log(2)))
        print("* size of N:", int(log(N) / log(2)))
        print("* m:", m, ", t:", t)

    # boneh_durfee
    if debug:
        print("=== running algorithm ===")
        start_time = time.time()

    solx, soly = boneh_durfee(pol, e, m, t, X, Y)

    # found a solution?
    if solx > 0:
        print("=== 找到解决方案 ===")
        if False:
            print("x:", solx)
            print("y:", soly)

        d = int(pol(solx, soly) / e)
        print("private key found: d =", d)
    else:
        print("=== no solution was found ===")

    if debug:
        print(("=== %s seconds ===" % (time.time() - start_time)))


if __name__ == "__main__":
    ############################################
    # How To Use This Script
    ##########################################
    N = 0xb12746657c720a434861e9a4828b3c89a6b8d4a1bd921054e48d47124dbcc9cfcdcc39261c5e93817c167db818081613f57729e0039875c72a5ae1f0bc5ef7c933880c2ad528adbc9b1430003a491e460917b34c4590977df47772fab1ee0ab251f94065ab3004893fe1b2958008848b0124f22c4e75f60ed3889fb62e5ef4dcc247a3d6e23072641e62566cd96ee8114b227b8f498f9a578fc6f687d07acdbb523b6029c5bbeecd5efaf4c4d35304e5e6b5b95db0e89299529eb953f52ca3247d4cd03a15939e7d638b168fd00a1cb5b0cc5c2cc98175c1ad0b959c2ab2f17f917c0ccee8c3fe589b4cb441e817f75e575fc96a4fe7bfea897f57692b050d2b
    e = 0x9d0637faa46281b533e83cc37e1cf5626bd33f712cc1948622f10ec26f766fb37b9cd6c7a6e4b2c03bce0dd70d5a3a28b6b0c941d8792bc6a870568790ebcd30f40277af59e0fd3141e272c48f8e33592965997c7d93006c27bf3a2b8fb71831dfa939c0ba2c7569dd1b660efc6c8966e674fbe6e051811d92a802c789d895f356ceec9722d5a7b617d21b8aa42dd6a45de721953939a5a81b8dffc9490acd4f60b0c0475883ff7e2ab50b39b2deeedaefefffc52ae2e03f72756d9b4f7b6bd85b1a6764b31312bc375a2298b78b0263d492205d2a5aa7a227abaf41ab4ea8ce0e75728a5177fe90ace36fdc5dba53317bbf90e60a6f2311bb333bf55ba3245f
    c = 0xa3bce6e2e677d7855a1a7819eb1879779d1e1eefa21a1a6e205c8b46fdc020a2487fdd07dbae99274204fadda2ba69af73627bdddcb2c403118f507bca03cb0bad7a8cd03f70defc31fa904d71230aab98a10e155bf207da1b1cac1503f48cab3758024cc6e62afe99767e9e4c151b75f60d8f7989c152fdf4ff4b95ceed9a7065f38c68dee4dd0da503650d3246d463f504b36e1d6fafabb35d2390ecf0419b2bb67c4c647fb38511b34eb494d9289c872203fa70f4084d2fa2367a63a8881b74cc38730ad7584328de6a7d92e4ca18098a15119baee91237cea24975bdfc19bdbce7c1559899a88125935584cd37c8dd31f3f2b4517eefae84e7e588344fa5

    # the hypothesis on the private exponent (the theoretical maximum is 0.292)
    delta = 0.25  # this means that d < N^delta

    # Lattice (tweak those values)
    # you should tweak this (after a first run), (e.g. increment it until a solution is found)
    m = 4  # 格的大小（越大越好，速度会变慢）
    example(N,e,delta,m)

Pell方程(连分数的应用)

设 D 是一个正整数且不是完全平方数，则佩尔方程 $x^{2} - D * y^{2} = 1$ 总有正整数解，如果 $(x_{1}, y_{1}) 是使 x_{1} 最小的解$ ，则每个解都可以通过取幂得到： $x_{k} + y_{k} \sqrt{D} = (x_{1} + y_{1} \sqrt{D})^{k} ， k = 1, 2, 3, . . .$

暴力求解

例：计算 $x^{2} - 10 * y^{2} = 1$

from gmpy2 import *
def Pell(D):
    x = 1
    y = 1
    while(1):
        x = iroot(D*y*y + 1,2)[0]
        if(pow(x,2) == D*y*y + 1):
            break
        y += 1
    return x,y
x,y = Pell(10)
print(x,y)

设 $\frac{p}{q}$ 是 $\sqrt{D}$ 的连分数渐进分数表示： $[a_{0}; a_{1}, a_{2}, a_{3}, . . .]$ 的渐进分数列，由连分数理论知存在 $i$ 使得 $(p_{i}, q_{i})$ 为佩尔方程的解。取其中最小的 $i$ ，将对应的 $(p_{i}, q_{i})$ 称为佩尔方程的基本解（最小解），记作 $(x_{1}, y_{1})$ ，则所有的解 $(x_{i}, y_{i})$ 可表示成如下形式： $x_{i} + y_{i} \sqrt{D} = (x_{1} + y_{1} \sqrt{D})^{i}$

一、有理连分数：

一个实数的简单连分数表示：

$x = a_{0} + \frac{1}{a_{1} + \frac{1}{a_{2} + \frac{1}{a_{3} + . . .}}}$

把简单连分数记为： $x = [a_{0}; a_{1}, a_{2}, a_{3} . . .]$

二、无理数的连分数有理逼近（解Pell方程时的情况）：

所有无限连分数都是无理数，而所有无理数都可以用一种精确的方式表示成无限连分数，可以用这种方法逼近，无理数的值。

可以证明，一个非完全平方数的平方根的连分数是以周期呈现的。如下：

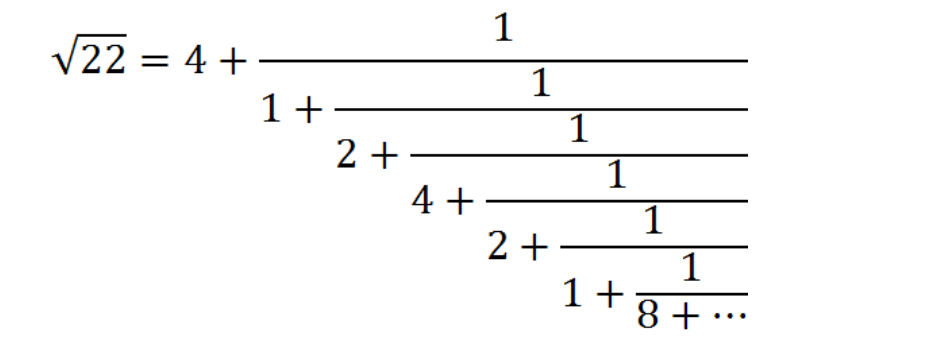
记为： $\sqrt{22} = [4; 1, 2, 4, 2, 1, 8, . . .]$

之后的计算结果就会以 <1,2,4,2,1,8> 为循环序列，周期性呈现。

还有个重要的特点：对于无理数的连分数 $x = [a_{0}; a_{1}, a_{2}, a_{3} ， . . . a_{n}]$ ，其循环一定是从 $a_{1}$ 开始的，且最后一个数 $a_{n}$ 一定是 2 倍的 $a_{0}$

三、求解Pell 方程的最小特解

将 $\sqrt{D}$ 写成连分数的形式： $\sqrt{D} = [a_{0}; a_{1}, a_{2}, . . ., a_{n - 1}, 2 a_{0}]$

设 $\frac{p}{q}$ 是 $\sqrt{D}$ 的连分数的渐进分数表示，记 $\frac{p}{q} = [a_{0}; a_{1}, a_{2}, . . ., a_{n - 1}]$ ，用连分数求渐进分数迭代计算即可。

如果记循环长度为 s，那么有如下结论：

1、如果 s 为偶数，最小特解为： $x_{0} = p ， y_{0} = q$

2、如果 s 为奇数，最小特解为： $x_{0} = 2 p^{2} + 1 ， y_{0} = 2 p q$

四、设计计算连分数的算法

接下来以 $\sqrt{22}$ 为例，解释如何计算 $\sqrt{D}$ 的连分数。

我们记当前展开为 $r_{i}$ ，那么首先 $r_{0} = \sqrt{22}$

$r_{0} = \sqrt{22} = 4 + \frac{1}{r_{1}} ， a_{0} = 4 ， \frac{1}{r_{1}} = \sqrt{22} - 4$

$r_{1} = \frac{\sqrt{22} + 4}{6} = 1 + \frac{1}{r_{2}} ， a_{1} = 1 ， \frac{1}{r_{2}} = \frac{\sqrt{22} - 2}{6}$

$r_{2} = \frac{\sqrt{22} + 2}{3} = 2 + \frac{1}{r_{3}} ， a_{2} = 2 ， \frac{1}{r_{3}} = \frac{\sqrt{22} - 4}{3}$

$r_{3} = \frac{\sqrt{22} + 4}{2} = 4 + \frac{1}{r_{4}} ， a_{3} = 4 ， \frac{1}{r_{4}} = \frac{\sqrt{22} - 4}{2}$

$r_{4} = \frac{\sqrt{22} + 4}{3} = 2 + \frac{1}{r_{5}} ， a_{4} = 2 ， \frac{1}{r_{5}} = \frac{\sqrt{22} - 2}{3}$

$r_{5} = \frac{\sqrt{22} + 2}{6} = 1 + \frac{1}{r_{6}} ， a_{5} = 1 ， \frac{1}{r_{6}} = \frac{\sqrt{22} - 4}{6}$

$r_{6} = \sqrt{22} + 4 = 8 + \frac{1}{r_{7}} ， a_{6} = 8 ， \frac{1}{r_{7}} = \sqrt{22} - 4$

计算出的连分数为： $\sqrt{22} = [4; < 1, 2, 4, 2, 1, 8 >]$

然后计算出其渐进分数得到： $\frac{197}{42} = [4; 1, 2, 4, 2, 1, 8]$ ，由于循环的长度为 6 是偶数，那么佩尔方程， $x^{2} - 22 y^{2} = 1 的最小特解是： x_{0} = 197 ， y_{0} = 42$

同理计算 $\sqrt{33}$ 得到其循环连分数为： $x = [5; 1, 2, 1, 10]$ ，循环长度 s = 4 ，最小特解为： $x = 23$ ， $y = 4$

根据上面的例子设计的连分数的算法：

我们记： $r_{0} = \sqrt{D} ， r_{i} = \frac{\sqrt{D} + b_{i}}{c_{i}}$

那么有： $a_{i} = [r_{i}] = [\frac{\sqrt{D} + b_{i}}{c_{i}}]$

新的 b ,c 为： $b_{i + 1} = c_{i} a_{i} - b_{i} ， c_{i + 1} = \frac{D - b_{i + 1}^{2}}{c_{i}}$

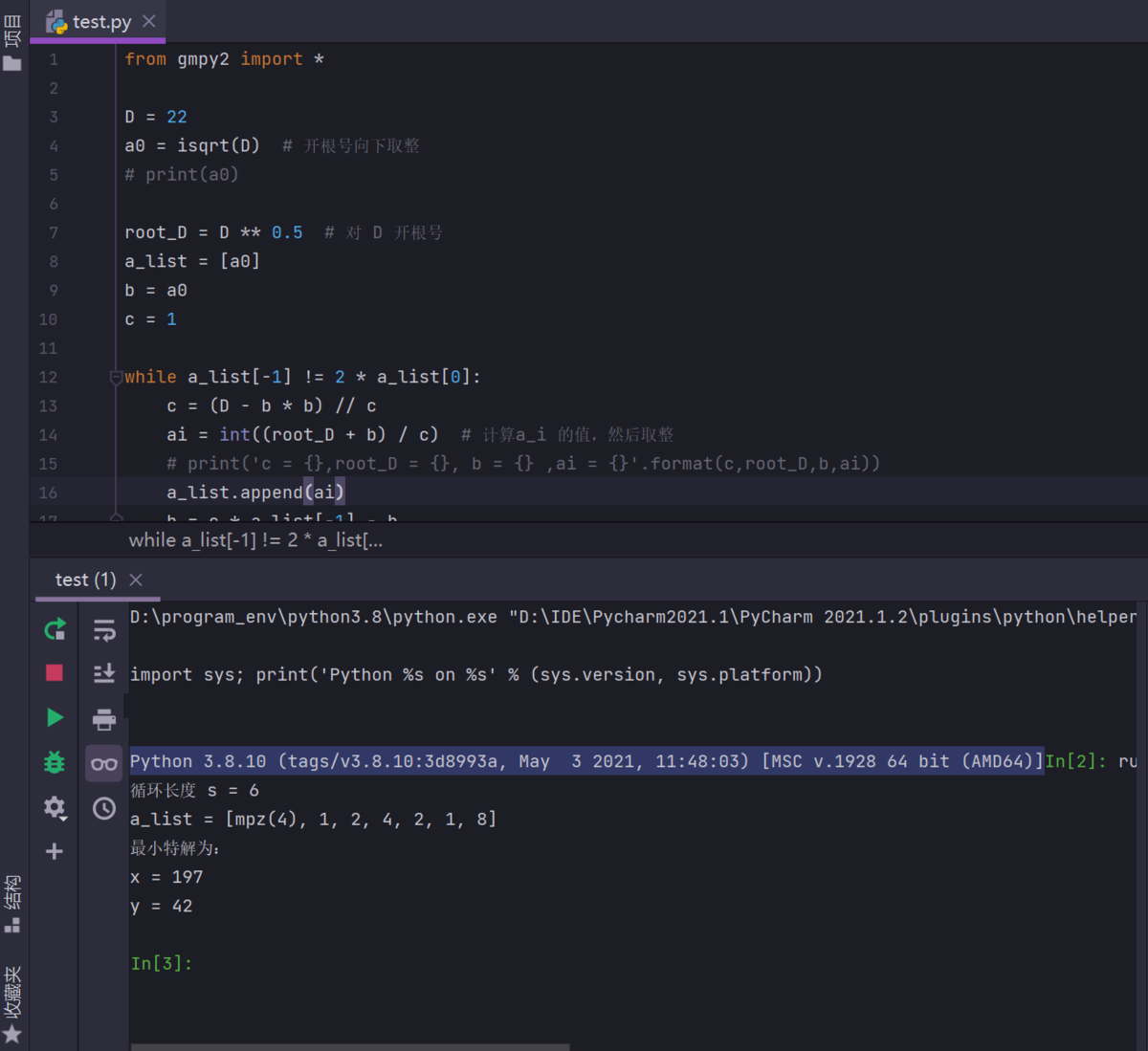
实现EXP：

from gmpy2 import *

D = 81421
a0 = isqrt(D)  # 开根号向下取整
print(a0)

root_D = D ** 0.5  # 对 D 开根号
a_list = [a0]
b = a0
c = 1

while a_list[-1] != 2 * a_list[0]:
    c = (D - b * b) // c
    ai = int((root_D + b) / c)  # 计算a_i 的值，然后取整
    # print('c = {},root_D = {}, b = {} ,ai = {}'.format(c,root_D,b,ai))
    a_list.append(ai)
    b = c * a_list[-1] - b


s = len(a_list) - 1
print("判断循环长度 s 为奇数还是偶数:",len(a_list) - 1)  # 判断循环长度 s 为奇数还是偶数
print(a_list)

# 以上计算无理数的连分数

# 以下计算连分数的渐进分数
def continued_fraction(sub_res):
    numerator, denominator = 1, 0
    for i in sub_res[::-1]:  # 从sublist的后面往前循环
        denominator, numerator = numerator, i * numerator + denominator
    return numerator, denominator  # 得到渐进分数的分母和分子，并返回


def sub_fraction(x):
    res = x
    res = list(map(continued_fraction, (res[0:i] for i in range(1, len(res) + 1))))  # 将连分数的结果逐一截取以求渐进分数
    return res


list = sub_fraction(a_list)
# print(list)

for (fenzi, fenmu) in list:
    if is_even(s):  # 如果是偶数
        x = fenzi
        y = fenmu
    else:           # 如果是奇数
        x = 2*pow(fenzi,2)+1
        y = 2*fenzi*fenmu
    if x ** 2 - D * (y ** 2) == 1:
        print('最小特解为：\nx = {}\ny = {}'.format(x, y))

测试执行 D=22 和 D=33

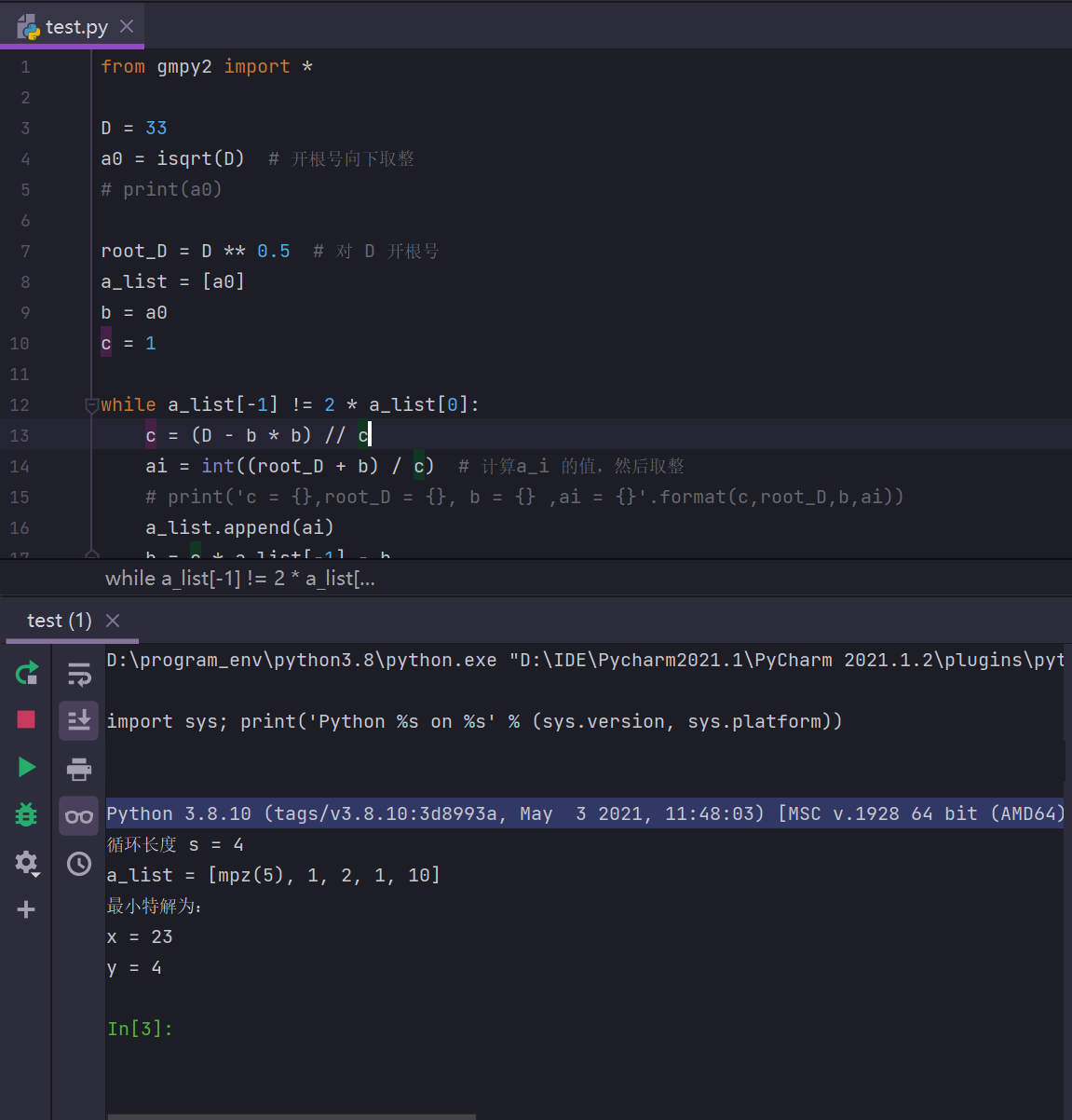
例题：[第一届数字空间安全攻防大赛] picproblem

assert 1301149798051259562945444365741194129602596348352064372203373*pow(x, 2) == 1175915431138623881271508290982969935822476052419526528443170552123*pow(y, 2) + 1301149798051259562945444365741194129602596348352064372203373

方程化简后得到： $x^{2} - 903751 * y^{2} = 1$

符合Pell方程的形式：套用上面的 exp得到解 x，y

构造不安全的私钥d（d,N不互素）

在 from Crypto.PublicKey import RSA 加密库中有函数 RSA.construct([n, e, d, p, q])

construct() 函数用于从有效的 RSA 组件的元组构造 RSA 密钥

在这个函数中会执行，对密钥一致性的各项安全检查，如下：

# Verify consistency of the key
    if consistency_check:

        # Modulus and public exponent must be coprime
        if e <= 1 or e >= n:
            raise ValueError("Invalid RSA public exponent")
        if Integer(n).gcd(e) != 1:
            raise ValueError("RSA public exponent is not coprime to modulus")

        # For RSA, modulus must be odd
        if not n & 1:
            raise ValueError("RSA modulus is not odd")

        if key.has_private():
            # Modulus and private exponent must be coprime
            if d <= 1 or d >= n:
                raise ValueError("Invalid RSA private exponent")
            if Integer(n).gcd(d) != 1:
                raise ValueError("RSA private exponent is not coprime to modulus")
            # Modulus must be product of 2 primes
            if p * q != n:
                raise ValueError("RSA factors do not match modulus")
            if test_probable_prime(p) == COMPOSITE:
                raise ValueError("RSA factor p is composite")
            if test_probable_prime(q) == COMPOSITE:
                raise ValueError("RSA factor q is composite")
            # See Carmichael theorem
            phi = (p - 1) * (q - 1)
            lcm = phi // (p - 1).gcd(q - 1)
            if (e * d % int(lcm)) != 1:
                raise ValueError("Invalid RSA condition")
            if hasattr(key, 'u'):
                # CRT coefficient
                if u <= 1 or u >= q:
                    raise ValueError("Invalid RSA component u")
                if (p * u % q) != 1:
                    raise ValueError("Invalid RSA component u with p")

    return key

CISCN 2023 badkey

题目：

from Crypto.Util.number import *
from Crypto.PublicKey import RSA
from hashlib import sha256
import random, os, signal, string

def proof_of_work():
    random.seed(os.urandom(8))
    proof = ''.join([random.choice(string.ascii_letters+string.digits) for _ in range(20)])
    _hexdigest = sha256(proof.encode()).hexdigest()
    print(f"sha256(XXXX+{proof[4:]}) == {_hexdigest}")
    print('Give me XXXX: ')
    x = input()
    if len(x) != 4 or sha256(x.encode()+proof[4:].encode()).hexdigest() != _hexdigest:
        print('Wrong PoW')
        return False
    return True

if not proof_of_work():
    exit(1)
    
signal.alarm(10)
print("Give me a bad RSA keypair.")

try:
    p = int(input('p = '))
    q = int(input('q = '))
    assert p > 0
    assert q > 0
    assert p != q
    assert p.bit_length() == 512
    assert q.bit_length() == 512
    assert isPrime(p)
    assert isPrime(q)
    n = p * q
    e = 65537
    assert p % e != 1
    assert q % e != 1
    d = inverse(e, (p-1)*(q-1))
except:
    print("Invalid params")
    exit(2)

try:
    key = RSA.construct([n,e,d,p,q])
    print("This is not a bad RSA keypair.")
    exit(3)
except KeyboardInterrupt:
    print("Hacker detected.")
    exit(4)
except ValueError:
    print("How could this happen?")
    from secret import flag
    print(flag)

比赛的时候分析到这一步了，但是没有深究如何去构造，而是一贯想着套脚本，这个问题需要改正！

构造符合 gcd(d,N) != 1 的私钥d

已知信息： $e * d \equiv 1 m o d (q - 1) * (p - 1) ， N = p * q$

我们需要构造出 d 和 N 存在公因数，假设： $g c d (d, N) = p$

利用公式： $d p \equiv d \mod (p - 1)$

得： $d p * p \equiv d * p \mod (p - 1) \equiv d + d (p - 1) m o d (p - 1) \equiv d m o d (p - 1)$

假设： $d = d p * p$ ，这样即满足 $g c d (d, N) = p$

推导代码编写：

先获取一个 512 比特的素数 p

$d p$ 可以通过计算逆元 dp = invert(e,p-1) 得到

由 $d p * p = d$ 代入 $e * d \equiv 1 m o d (q - 1) * (p - 1)$ 得：

$e * d p * p \equiv 1 m o d (q - 1) * (p - 1) = 1 + k * (q - 1) * (p - 1)$

得： $(e * d p * p - 1) / / (p - 1) = k * (q - 1)$

通过比较大小可以推测：k的值大致在 e 的大小附近，爆破 k 值即可得到 q

再检测 q 的值是否满足为 512 比特大小以及为素数的要求，满足的话，我们就找到了一个符合 $d p * p = d$ 的私钥 p,q值。即这时的 $g c d (d, N) = p$

EXP:

import socket
from gmpy2 import *
from Crypto.Util.number import *
from hashlib import sha256
import string
from tqdm.auto import tqdm

def get_p_q():
    while 1:
        e = 65537
        p = getPrime(512)
        dp = invert(e, p - 1)
        num = (e * dp * p - 1) // (p - 1)
        for i in range(e, 1, -1):
            if num % i == 0:
                q = (num // i) + 1
                if q.bit_length() == 512 and is_prime(q):
                    return p, q


def sha256_check(key,num):
    # num = '2f83fe488e1b69ba260001ca74a23c2e34e3031ccf711d0fe464597b90ee95da'
    # key = 'LJ5WRugTd6yCX7qy'
    stringlist = string.ascii_letters + string.digits
    for a in tqdm(stringlist):
        for b in stringlist:
            for c in stringlist:
                for d in stringlist:
                    flag = a + b + c + d + key
                    md5_value = sha256((flag).encode()).hexdigest()
                    # print(md5_value)
                    if md5_value == num:
                        return a+b+c+d+'\n'
                    else:
                        continue

ip_port = ('node4.anna.nssctf.cn', 28873)
sk = socket.socket()
# sk.settimeout(20)
sk.connect(ip_port)
# sk.settimeout(None)
data = sk.recv(1024).decode()
print(data)

key = data[12:28]
num = data[33:97]

key_num = sha256_check(key,num)
print(key_num)

sk.sendall(key_num.encode())

data = sk.recv(1024).decode()
print(data)


p, q = get_p_q()

sk.sendall((str(p)+'\n').encode())
data = sk.recv(1024).decode()
print(data)

sk.sendall((str(q)+'\n').encode())
data = sk.recv(1024).decode()
print(data)

data = sk.recv(1024).decode()
print(data)
data = sk.recv(1024).decode()
print(data)