LFSR 线性反馈移位寄存器

N1Key2024/5/5大约 3 分钟

LFSR 原理

线性反馈移位寄存器（LFSR）归属于移位寄存器（FSR）,除此之外还有非线性移位寄存器（NFSR）。移位寄存器是流密码产生密钥流的一个主要组成部分。

$G F (2)$ 上一个n级反馈移位寄存器由与一个，如下图所示。

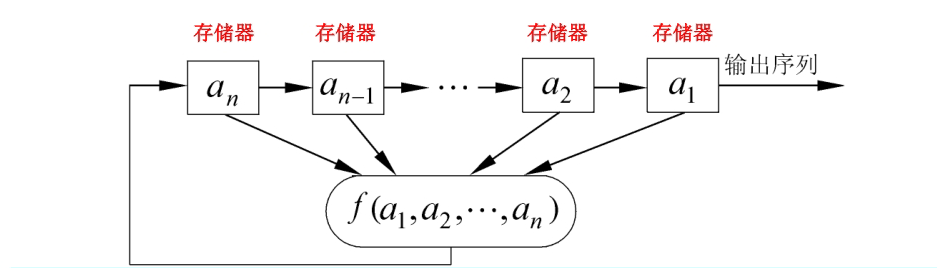
移位寄存器的三要素：

初始状态： 由用户确定
反馈函数： $f (a_{1}, a_{2}, . . ., a_{n})$ 是n元布尔函数，即函数的自变量和因变量只取0和1这两个可能值
输出序列

如果反馈函数是线性的，那么我们称其为 LFSR，如下图所示：

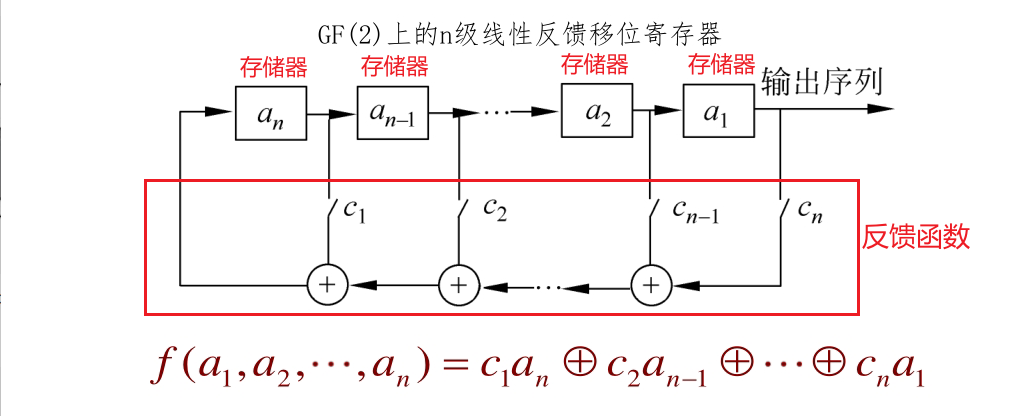
LFSR的输出序列{ $a_{n}$ }满足:

$f (a_{1}, a_{2}, . . ., a_{n}) = c_{1} a_{n} \oplus c_{2} a_{n - 1} \oplus . . . \oplus c_{n} a_{1}$

$a_{n + 1} = c_{1} a_{n} \oplus c_{2} a_{n - 1} \oplus . . . \oplus c_{n} a_{1}$
$a_{n + 2} = c_{1} a_{n + 1} \oplus c_{2} a_{n} \oplus . . . \oplus c_{n} a_{2}$
.....
$a_{n + i} = c_{1} a_{n + i - 1} \oplus c_{2} a_{n + i - 2} \oplus . . . \oplus c_{n} a_{i}$
(i = 1,2,3,...)

举例：

下面是一个5级的线性反馈移位寄存器，其初始状态为 $(a_{1}, a_{2}, . . ., a_{n}) = (1, 0, 0, 1, 1)$

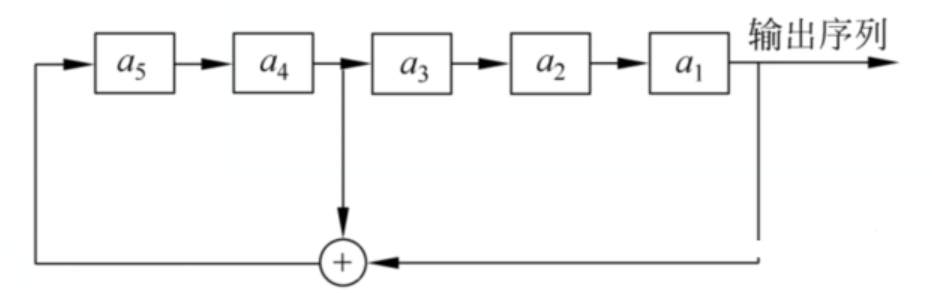
反馈函数为： $a_{5 + i} = a_{3 + i} \oplus a_{i}$ ，(i = 1,2,...)
可以得到输出序列为：

100110…

周期为31。

对于 n 级线性反馈移位寄存器，最长周期为 $2^{n} - 1$ （排除全零）。达到最长周期的序列一般称为 m 序列

已知反馈函数和输出序列，逆推求初始状态

例题1 2018 强网杯 Streamgame1

题目：

from flag import flag
assert flag.startswith("flag{")
assert flag.endswith("}")
assert len(flag) == 25


def lfsr(R, mask):
    output = (R << 1) & 0xffffff
    i = (R & mask) & 0xffffff
    lastbit = 0
    while i != 0:
        lastbit ^= (i & 1)  # 按位异或运算，得到输出序列
        i = i >> 1
    output ^= lastbit  # 将输出值写入 output的后面
    return output, lastbit


R = int(flag[5:-1], 2)  # flag为二进制数据
mask = 0b1010011000100011100

f = open("key", "ab")  # 以二进制追加模式打开
for i in range(12):
    tmp = 0
    for j in range(8):
        (R, out) = lfsr(R, mask)
        tmp = (tmp << 1) ^ out
    f.write(chr(tmp))  # 将lfsr输出的序列每8个二进制为一组，转化为字符，共12组
f.close()

考点:

def lfsr(R,mask):
    output = (R << 1) & 0xffffff  
    i=(R&mask)&0xffffff          
    lastbit=0
    while i!=0:
        lastbit^=(i&1)           
        i=i>>1     # R和mask进行异或操作，得到输出序列值
    output^=lastbit     #将输出值设置为output的最后一位
    return (output,lastbit)

题目已知条件为 flag 长度为19bits,mask 长度也为19bits.

由LFSR的输出序列{ $a_{n}$ }满足的条件:

$a_{n + i} = c_{1} a_{n + i - 1} \oplus c_{2} a_{n + i - 2} \oplus . . . \oplus c_{n} a_{i}$ $(i = 1, 2, 3, . . .)$

可知，输出值 $a_{n + i}$ 的结果与c的值相关，即题目中的 mask。只有当c的值为1时， $c_{1} a_{n + i - 1}, . . ., c_{n} a_{i}$ 的值才可能为1

题目中mask中只有第（3，4，5，9，13，14，17，19）位为1，其余都是0

注：(mask这里右边才是第一位，从右往左增大)

现在我们的目的就是为了求出前19位seed的值，而我们已知了seed后面输出序列的值（题目中给的附件key.txt）。那么我们逆推就能得到seed的值了。lfsr(R,mask)函数执行的是19bits的值。那么我们获取到输出序列前19bits值，即：key = 0101010100111000111

现在需要计算 $a_{19}$ 的值，假设我们将 R = $a_{19} 010101010011100011$ 作为初始序列，进行lfsr(R,mask)运算，那么我们将得到输出值为 key[-1]=1。

1 = $a_{19}$ ^(R[-3])(R[-4])^(R[-5])(R[-9])^(R[-13])(R[-14])^(R[-17])

得1 = $a_{19}$ ^0 ，得到 $a_{19}$ =1

同理：R = $a_{18} a_{19} 01010101001110001$ 的输出值为 key[-2]=1，求得 $a_{18}$ =1