曲线

知识点

映射

在代数几何中，如果存在一个映射将一条曲线上的点映射到另一条曲线上的点，且这个映射保持曲线上点的数量不变，那么我们称这个映射是一个保持曲线阶不变的映射。换句话说，如果有两条曲线 $C_1$​ 和 $C_2$​，存在一个一一对应的映射 $f:C_1\to C_2$​，使得对于 $C_1$​ 上的任意点 $P$，其映射点 $f(P)$ 在$C_2$​ 上，并且映射 $f$ 是双射的，那么我们称这个映射保持曲线的阶不变。

简单来说，这意味着两条曲线之间存在一种一一对应的关系，通过这个映射，我们可以保持曲线上的点的数量不变。这种性质在研究曲线的结构和性质时非常重要。

奇异椭圆曲线

相关学习论文 ：

1、 Elliptic Curves: Number Theory and Cryptography第二章 2.10 Singular Curves,P59-P62

2、 The Arithmetic of Elliptic Curves, pp 55-58

在代数几何和椭圆曲线理论中，当椭圆曲线参数 $a,b$ 满足判别式：$\mathrm{△}=4a^3+27b^2=0$ 时，表示这是一条奇异椭圆曲线（Singular elliptic curve），指的是具有奇异点的椭圆曲线。奇异点是指曲线上某一点的局部性质与曲线的平滑部分不同，通常可以通过观察导数来检测出来。在椭圆曲线的情况下，奇异点通常是曲线上的特殊点，它们导致了曲线的局部性质的改变。

在椭圆曲线上，奇异点可以分为几类，包括尖点、节点和无理点等。尖点是曲线上的一个奇异点，其坐标可以通过特定的模运算来表示，而节点是曲线上一个点与自身相交的点，这会导致曲线在该点处的切线不唯一。无理点则是曲线上的一个点，其坐标不是有理数。

奇异椭圆曲线在代数几何和数论中都具有重要的作用。尽管大多数情况下，我们处理的椭圆曲线都是光滑的（即没有奇异点），但有时需要考虑奇异椭圆曲线，特别是当我们研究椭圆曲线上的点的结构和性质时。

注：(奇异点可以理解为高数中的导数不存在的点)

• 尖点（Cusp）

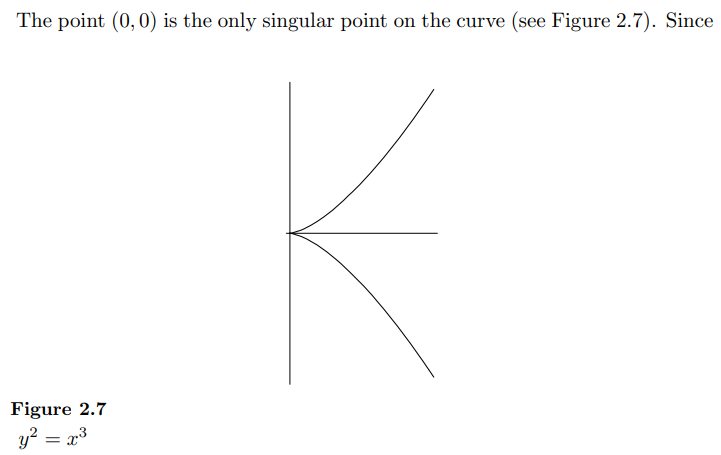
尖点是曲线上的一个奇异点，在该点处曲线具有“尖锐”的转折。对于一个方程表示的曲线，如果在某个点处导数趋向于无穷大或者在该点处曲线无法定义一个明确的切线，则这个点可能是一个尖点。

几何上，尖点看起来像一个尖锐的角。例如，在曲线 $y^2=x^3$ 上，原点 $(0,0)$ 是一个尖点。

image-20240704150119903

• 节点（Node）

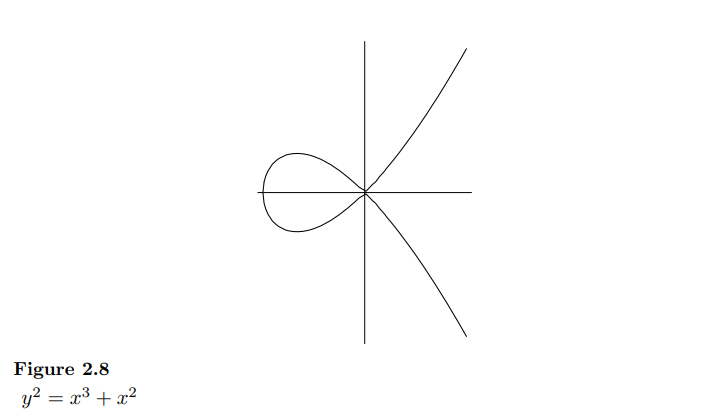
节点是曲线上另一种类型的奇异点，它通常是曲线在该点处相交的地方。节点可以认为是两个光滑分支在该点相交，且在该点处曲线具有两个不同的切线。

几何上，节点看起来像一个交叉点。例如，在曲线 $y^2=x^2(x+1)$ 上，原点 $(0,0)$是一个节点，因为在该点处曲线的两个分支相交。

image-20240704150227357

超奇异椭圆曲线

1、超奇异椭圆曲线（Supersingular Elliptic Curve）：在特征为 $p$ 的有限域 $F_p$ 上，一条椭圆曲线 $E$ 是超奇异的，如果其 $Frobenius$ 映射的特征多项式是 $x^2+p$。

2、非超奇异椭圆曲线（Ordinary Elliptic Curve）： 在特征为 $p$ 的有限域 $F_p$ 上，一条椭圆曲线 $E$ 是非超奇异的，如果其 $Frobenius$ 映射的特征多项式不是 $x^2+p$。

超奇异椭圆曲线判别方法

Trace of Frobenius计算椭圆曲线的 Frobenius endomorphism（同态） 的 trace（迹），记作 $t$。对于特征 $p$ 的有限域 $F_p$，椭圆曲线 $E$ 的特征多项式为 $x^2-tx+p$。 根据 $t$ 的值判断：

• 如果 $t=0$，则椭圆曲线是超奇异的。
• 如果 $t\ne 0$，则椭圆曲线是非超奇异的。

SageMath 提供了一些内置函数 trace_of_frobenius() 来计算椭圆曲线的 Frobenius trace $t$ :

E = EllipticCurve(F, [a, b])

# 计算 Frobenius trace t
t = E.trace_of_frobenius()

SageMath 提供了查看 Frobenius 映射特征多项式的函数 frobenius_polynomial()

E = EllipticCurve(F, [a, b])

# 获取 Frobenius 映射的特征多项式
frobenius_poly = E.frobenius_polynomial()

Frobenius迹的具体含义

在有限域 $F_p$ 上，给定一条椭圆曲线 $E$，我们可以定义 Frobenius同态（Frobenius endomorphism），它是一个从椭圆曲线到自身的映射。Frobenius迹 $t$ 是这个映射的特征多项式 $x^2-tx+p$ 中的系数。

具体来说，Frobenius 迹 $t$ 满足以下关系：

$t=p+1-N$

其中 $N$ 是椭圆曲线 $E$ 在有限域 $F_p$ 上的点的个数。

genus 0 curves（亏格为0的曲线）

在代数几何中，曲线的“genus”（亦称为“维数”或“种数”）是一个重要的概念，它描述了曲线的几何形状。在这个背景下，genus 0 曲线指的是代数曲线，其genus为0。

对于实数域上的曲线，genus 0 意味着曲线可以视为是一个连通的不可约曲线，没有“洞”或“孔”。换句话说，它可以在平面上连续变形成一个球面（即球面的genus也是0）。

代数曲线的genus可以解释为“洞”的数量。Genus为0表示曲线没有洞，Genus为1表示有一个洞，以此类推。

在曲面理论中，"genus" 通常被翻译为 "亏格" 或 "缺失"。亏格是描述曲面的一种拓扑不变量，表示曲面的拓扑性质中“缺失”的部分。对于一般的曲面，亏格可以理解为“孔”的数量，比如球面的亏格为0（因为没有孔），环面的亏格为1（因为有一个孔），双环面的亏格为2，以此类推。

1. 曲线 $x^2-D{y}^2=1$

注

相关论文：关于循环群、有限域和离散对数问题的说明

曲线 $x^2-D{y}^2=1$ ，当D是一个平方数时，该曲线是一个亏格为0的曲线，设 $q$ 为奇素数或奇素数的幂，D是 $F_q$ 上的一个非零元素，$C$ 表示曲线方程的解集 $(x,y)\in F_q\ast F_q$

$C$ 的元素是亏格为0的代数曲线上的仿射点，我们定义加法 “+” 运算如下：

$(x_1,y_1)+(x_2,y_2)=(x_1{x}_2+D{y}_1{y}_2,x_1{y}_2+x_2{y}_1)$

引理：$(C,+)$ 是一个阿贝尔群

设 $\lambda (a)$ 表示 $a$ 是模 $q$ 的二次剩余，则:

$$\lambda (a)=\{\begin{array}{rcl}1,& & a\mathrm{是}\mathrm{模}q\mathrm{的}\mathrm{二}\mathrm{次}\mathrm{剩}\mathrm{余}\\ -1,& & a\mathrm{是}\mathrm{模}q\mathrm{的}\mathrm{二}\mathrm{次}\mathrm{非}\mathrm{剩}\mathrm{余}\\ 0,& & a=0\end{array}$$

现在我们可以确定 $C$ 的群结构。

定理：$(C,+)$ 是一个 $q$ 阶的循环群——$\lambda (D)$

将曲线上的离散对数问题简化为 $F_q$ 中的离散对数问题

情况1：当 $\lambda (D)=-1$时

有：

设 $f(W)=W^2-D\in F_q[W]$ ，$f(W)$ 为有限域 $F_q$ 上的一个不可约多项式。

代码写法为：

R.<w> = GF(q^2, modulus=w**2 - D)

modulus（模数）在这个函数中的作用是指定一个多项式，它定义了在 GF(p)中进行加法和乘法运算时所使用的模数。通常，这个多项式是 GF(p)上的一个不可约多项式，这意味着它不能被分解为两个或更多次数更低的多项式的乘积。使用模数的好处之一是它可以限制结果的大小，使得它们保持在一个有限的范围内。

因此，我们可以定义一个(bijective map)双射映射，代表着将椭圆曲线上的点映射到另一个椭圆曲线上的点是一一对应的。

映射公式为：$\varphi :(x,y)⟼x+yW$ ，此时 $C$ 是一个 $q+1$ 阶的循环群。

注：其中 $(x+yW)\in F_{q^2}$

例题：例题：[2022 SEETF] The True ECC

情况2：当 $\lambda (D)=1$时

设 $a\in F_q$ 的 $D$ 的一个平方根（即 $a^2=D,a=\sqrt{D}$），我们可以将等式 $x^2-D{y}^2=1$ 改写成 $(x-ay)(x+ay)=1$。

设 $u=x-ay$ ，$v=x+ay$，

然后有：$x=\frac{u+v}{2}$ ，$y=\frac{v-u}{2}$

因此，我们可以定义一个(bijective map)双射映射，映射公式为： $\varphi :(x,y)⟼x-ay$ ，此时 $C$ 是一个 $q-1$ 阶的循环群。

例题：Ellipse Curve Cryptography(椭圆曲线加密)

常见曲线

• 曲线数据库 https://www.hyperelliptic.org/EFD/

Weierstrass curves(魏尔斯特拉斯曲线)

我们在椭圆曲线加密中使用的曲线方程一般都是Weierstrass曲线方程，下面我们来看一下椭圆曲线的定义。

设 $K$ 是一个域，可以认为是实数域，在密码学中常用的 $K$ 是有限域。$\overline{K}$ 是 $K$ 的扩展域集合。使用 $E/K$ 表示定义在域 $K$ 上的曲线 $E$。

Weierstrass曲线方程的标准形式：

• $y^2+a_{1}xy+a_{3}y=x^3+a_2{x}^2+a_{4}x+a_6$ ，$a_i\in K$

一般方程形式：

• $y^2=x^3+ax+b(modp)$ ，曲线参数都是在有限域 $F_p$ 上的， 且满足 $4a^3+27b^2\ne 0(modp)$ ，即在密码学中我们选取的曲线要求是非奇异椭圆曲线。

我们在 sagemath 中能构建椭圆曲线方程的函数 EllipticCurve() 构建的是 Weierstrass curves 。

在椭圆曲线 $E$ 上定义加法运算 “$+$ ” ，设 $P(x_1,y_1),Q(x_2,y_2)\in E$，$O$ 是椭圆曲线上的无穷远点，则

（1）$P+O=P$ （$O$为无穷远点）；

（2）若 $x_1=x_2,y_1=-y_2$，则 $P+Q=O$ ；

（3）当 $P+Q=(x_3,y_3)$ ，其中

$$\{\begin{array}{l}{x}_3={\lambda }^2-x_1-x_2\\ y_3=\lambda (x_1-x_3)-y_1\end{array}$$$$\lambda =\{\begin{array}{ll}\frac{y_2-y_1}{x_2-x_1},& \mathrm{如}\mathrm{果}P\ne Q\\ \frac{3x_1^2+a}{2y_1},& \mathrm{如}\mathrm{果}P=Q\end{array}$$

如果 $P+Q=O$,则记 $Q=-P$ ，并称 $-P$ 为 $P$ 的逆元。

一般地，我们将 $\underset{n\mathrm{次}}{\underbrace{P+P+\cdot \cdot \cdot +P}}$ 记为 $nP$ ，即 $np=$ $\underset{n\mathrm{次}}{\underbrace{P+P+\cdot \cdot \cdot +P}}$，同时，定义：$0P=O$（单位元）

Montgomery curves(蒙哥马利曲线)

曲线方程：

• $M_{A,B}：B{y}^2=x^3+A{x}^2+x$

点加：

$(x_1,y_1)+(x_2,y_2)=(x_3,y_3)$

其中：

$x_3=B\ast (\frac{y_2-y_1}{x_2-x_1}{)}^2-A-x_1-x_2$ ， $y_3=(\frac{y_2-y_1}{x_2-x_1})\ast (x_1-x_3)-y_1$

倍乘：

$2(x_1,y_1)=(x_3,y_3)$

其中：

$\alpha =(3x_1^2+2A{x}_1+1)/(2B{y}_1)$

$x_3=B{\alpha }^2-A-2x_1$ ，$y_3=\alpha (x_1-x_3)-y_1$

映射：

• 映射为Weierstrass 曲线：$M_{A,B}⟼E_{a,b}:v^2=u^3+au+b$

其中：$(x,y)⟼(u,v)=(\frac{x}{B}+\frac{A}{3B},\frac{y}{B})$

$a=\frac{3-A^2}{3B^2}$ ，$b=\frac{2A^3-9A}{27B^3}$

理论知识参考 wiki

Edwards Curves(爱德华兹曲线)

曲线方程的形式1：

• $E_{c,d}：x^2+y^2=c^2(1+d{x}^2{y}^2)$ ，$d\in K\mathrm{\setminus }\{0,1\}$

曲线方程的形式2：

• $E_d：x^2+y^2=1+d{x}^2{y}^2$

点加：

$$(x_1,y_1)+(x_2,y_2)=(\frac{x_1{y}_2+x_2{y}_1}{c(1+d{x}_1{x}_2{y}_1{y}_2)},\frac{y_1{y}_2-x_1{x}_2}{c(1-d{x}_1{x}_2{y}_1{y}_2)})$$

点的取反：

曲线上任意点 $(x,y)$ 的相反点为：$(-x,y)$

映射：

• 映射为 Weierstrass 曲线：$E_d：x^2+y^2=1+d{x}^2{y}^2⟼E_{a2,a4}:v^2=u^3+2(d+1)u^2+(d-1{)}^{2}u)$

$$(x,y)⟼(u,v)=(\frac{A}{x^2},\frac{-2A}{x^3})$$

其中： $A=2y-(2dy+d+1)x^2+2$

相关论文 Edwards Elliptic Curves 理论在第 22—23 页

• 将$E_{c,d}：x^2+y^2=c^2(1+d{x}^2{y}^2)$ 映射为： $E_d：x^2+y^2=1+d{x}^2{y}^2$

相关论文 Faster addition and doubling on elliptic curves 理论在第 5 页

映射的实现基于有限域p，令 $d=d_1\ast c_1^4$，$x=\frac{x_1}{c_1}，y=\frac{y_1}{c_1}$

则有：$x_1^2+y_1^2=c_1^2(1+d_1{x}_1^2{y}_1^2)⟼x^2+y^2=1+d{x}^2{y}^2$

代码实现：

assert P[0] ^ 2 + P[1] ^ 2 - c ^ 2 * (1 + d * P[0] ^ 2 * P[1] ^ 2) == 0
# https://eprint.iacr.org/2007/286.pdf page 5
F = GF(p)
d = F(d) * F(c) ^ 4

def phi(P):
    return (P[0] / c, P[1] / c)

P = phi(P)
Q = phi(Q)
assert P[0] ^ 2 + P[1] ^ 2 - (1 + d * P[0] ^ 2 * P[1] ^ 2) == 0

例题： 1.Edwards Curves DLP

Twisted Edwards Curves(扭曲的爱德华兹曲线)

曲线方程：

• $E_{a,d}：a{x}^2+y^2=1+d{x}^2{y}^2$

点加：

$$(x_1,y_1)+(x_2,y_2)=(\frac{x_1{y}_2+x_2{y}_1}{1+d{x}_1{x}_2{y}_1{y}_2},\frac{y_1{y}_2-a{x}_1{x}_2}{1-d{x}_1{x}_2{y}_1{y}_2})$$

倍乘：

$2(x_1,y_1)=(x_3,y_3)$

其中：

$$x_3=\frac{2x_1{y}_1}{1+d{x}_1^2{y}_1^2}=\frac{2x_1{y}_1}{a{x}_1^2+y_1^2}$$$$y_3=\frac{y_1^2-a{x}_1^2}{1-d{x}_1^2{y}_1^2}=\frac{y_1^2-a{x}_1^2}{2-a{x}_1^2-y_1^2}$$

点的取反：

曲线上任意点 $(x,y)$ 的相反点为：$(-x,y)$

映射：

• 映射为 Montgomery 曲线

$E_{a,d}⟼M_{A,B}：B{v}^2=u^3+A{u}^2+u$

其中：

$A=\frac{2(a+d)}{a-d}，B=\frac{4}{a-d}$

$$u=\frac{1+y}{1-y}，v=\frac{1+y}{x(1-y)}=\frac{u}{x}$$

相关论文 Twisted Edwards Curves 理论在第 4 页

这篇论文中还提到了，将扭曲的爱德华兹曲线双有理等价于另一种扭曲的爱德华兹曲线的方法。（mark⭐）

Hessian Curves(海森曲线)

曲线方程：

• $H_{c,d}：x^3+y^3+c=dxy$ ，$d\in F$ 有限域 ，$c\ne 0,d^3\ne 27c$

点加：

$$(x_1,y_1)+(x_2,y_2)=(\frac{y_1^2{x}_2-y_2^2{x}_1}{x_2{y}_2-x_1{y}_1},\frac{x_1^2{y}_2-x_2^2{y}_1}{x_2{y}_2-x_1{y}_1})$$

倍乘：

$$2(x_1,y_1)=(\frac{y_1(c-x_1^3)}{x_1^3-y_1^3},\frac{x_1(c-y_1^3)}{x_1^3-y_1^3})$$

点的取反：

曲线上任意点 $(x,y)$ 的相反点为：$(y,x)$

映射：

• 将 Hessian Curves（海森曲线）映射为 Weierstrass 曲线：$$H：x^3+y^3+1=3Dxy⟼E_{a,b}：v^2=u^3-27D(D^3+8)\ast u+54(D^6-20D^3-8)$$（其中 $3D=d$ ，令 $D=d/3$）

坐标的映射为：

$$(x,y)⟼(u,v)=(-9D^2+Bx,3B(y-1))$$

其中 $B=\frac{12(D^3-1)}{Dx+y+1}$

参考wiki介绍：Hessian form of an elliptic curve

另一篇参考论文：Hessian Elliptic Curves and Side-Channel Attacks

例题： https://blog.maple3142.net/2023/07/09/cryptoctf-2023-writeups/#barak

Twisted Hessian Curves(扭曲的海森曲线)

当 a = 1 时，即为海森曲线；所以海森曲线是扭曲的海森曲线的一个特例

曲线方程：

• $H_{a,d}：a{x}^3+y^3+1=dxy$ ，$a(d^3-27a{)}^3\ne 0$

点加：

$$(x_1,y_1)+(x_2,y_2)=(\frac{x_1-y_1^2{x}_2{y}_2}{a{x}_1{y}_1{x}_2^2-y_2},\frac{y_1{y}_2^2-a{x}_1^2{x}_2}{a{x}_1{y}_1{x}_2^2-y_2})$$

倍乘：

$$2(x,y)=(\frac{x-y^{3}x)}{ay{x}^3-y},\frac{y^3-a{x}^3)}{ay{x}^3-y})$$

点取反：

点 $(x,y)$ 的相反点为 $(\frac{x}{y},\frac{1}{y})$

映射：

• 将 Twisted Hessian Curves（扭曲的海森曲线）映射为 Weierstrass 曲线：

$$H_{a,d}：a{x}^3+y^3+1=dxy⟼E_{a_4,a_6}：v^2=u^3-\frac{d^4+216da}{48}\ast u+\frac{d^6-540d^{3}a-5832a^2}{864}$$$$(x,y)⟼(u,v)=(\frac{xA}{3}-\frac{d^2}{4},\frac{A(1-y)}{2})$$

其中：$A=\frac{d^3-27a}{3+3y+dx}$

def THessian_to_Weierstrass(P):  
    x, y = P  
    A = (d ** 3 - 27 * a) * pow(3 + 3 * y + d * x, -1, p)  
    u = (x * A) * pow(3, -1, p) - (d ** 2) * pow(4, -1, p)  
    v = A * (1 - y) * pow(2, -1, p)  
    return (u, v)

a4 = -(d ** 4 + 216 * d * a) * pow(48, -1, p)  
a6 = (d ** 6 - 540 * d ** 3 * a - 5832 * a ** 2) * pow(864, -1, p)

相关论文 Elliptic Curves, Group Law, and Efficient Computation 第 40页

参考 wiki：https://en.wikipedia.org/wiki/Twisted_Hessian_curves

Huff Curves(哈夫曲线)

曲线方程：

• $x(a{y}^2-1)=y(b{x}^2-1)$

点加：

$$(x_1,y_1)+(x_2,y_2)=(\frac{(x_1+x_2)(1+a{y}_1{y}_2)}{(1+b{x}_1{x}_2)(1-a{y}_1{y}_2)},\frac{(y_1+y_2)(1+b{x}_1{x}_2)}{(1-b{x}_1{x}_2)(1+a{y}_1{y}_2)})$$

倍乘：

$$2(x_1,y_1)=(\frac{2x_1(1+a{y}_1^2)}{(1+b{x}_1^2)(1-a{y}_1^2)},\frac{2y_1(1+b{x}_1^2)}{(1-b{x}_1^2)(1+a{y}_1^2)})$$

点取反：

$(x,y)$ 的取反点为 $-(x,y)$ ，代码上实现为：

-G = mul(G.order - 1, G)

映射：

• 映射为 Weierstrass 曲线形式：

$x(a{y}^2-1)=y(b{x}^2-1)⟼v^2=u^3+a_2{u}^2+a_{4}u$

其中：

$$u=\frac{bx-ay}{y-x},v=\frac{b-a}{y-x}$$$$a_2=a+b,a_4=ab$$

例题：

2023 DASCTF CBCTF - CB curve

extended Jacobi quartic curve(扩展的雅可比四次曲线)

曲线的一般方程：

• $J_{d,a}：y^2=d{x}^4+2a{x}^2+1$

点加：

$(x_1,y_1)+(x_2,y_2)=(x_3,y_3)$

$$x_3=\frac{x_1{y}_2+y_1{x}_2}{1-d{x}_1^2{x}_2^2}$$$$y_3=\frac{(y_1{y}_2+2a{x}_1{x}_2)(1+d{x}_1^2{x}_2^2)+2d{x}_1{x}_2(x_1^2+x_2^2)}{(1-d{x}_1^2{x}_2^2{)}^2}$$

映射：

• 映射为 Weierstrass 曲线：

$J_{d,a}⟼E_W：v^2=u^3-4a{u}^2+(4a^2-4d)u$

$$(x,y)⟼(u,v)=(\frac{2y+2}{x^2}+2a,\frac{4y+4}{x^3}+\frac{4a}{x})$$

$E_W⟼J_{d,a}：$

$$(u,v)⟼(x,y)=(2\frac{u}{v},2(u-2a)\frac{u^2}{v^2}-1)$$

相关论文 Elliptic Curves, Group Law, and Efficient Computation 第 38-39 页