MatheMatics(数学)

N1Key2024/2/18大约 17 分钟

LATTICES(格)

Vectors(向量)

v = (2,6,3)、w = (1,0,0) 和 u = (7,7,2)，计算 $3 (2 v - w) * 2 u$ 。

按照线性代数的向量公式计算即可得到：702

v = vector([2, 6, 3])
w = vector([1, 0, 0])
u = vector([7, 7, 2])
print((3 * (2 * v - w)) * (2 * u))

Size and Basis(大小和基)

基是指一组线性无关的向量

计算向量的模(大小)：v = (4, 6, 2, 5)

$| V | = \sqrt{4^{2} + 6^{2} + 2^{2} + 5^{2}} = 9$

sage: v = vector([4,6,2,5])
sage: v.norm()
9

Gram Schmidt(施密特正交化)

用 sagemath 中有的函数 gram_schmidt() 计算施密特正交化

sage参考资料：

https://doc.sagemath.org/html/en/reference/matrices/sage/matrix/matrix2.html#sage.matrix.matrix2.Matrix.gram_schmidt

#sage
from sage.all import *

A = matrix(QQ,[[4,1,3,-1],
              [2,1,-3,4],
              [1,0,-2,7],
              [6,2,9,-5]])
G,M = A.gram_schmidt()	# 施密特正交化
print(G)

$(\begin{array}{rrrr} 4 & 1 & 3 & - 1 \\ \frac{70}{27} & \frac{31}{27} & - \frac{23}{9} & \frac{104}{27} \\ - \frac{287}{397} & - \frac{405}{397} & \frac{799}{397} & \frac{844}{397} \\ - \frac{1456}{4023} & \frac{273}{298} & \frac{1729}{8046} & \frac{455}{4023} \end{array})$

273 / 298 = 0.91611(四舍五入)

What's a Lattice?（什么是格子）

给定一组线性无关向量 $v_{1}, v_{2}, . . ., v_{n} \in R^{m}$ ，由这组向量生成的格 L 是一组具有整数系数的线性无关向量 $v_{1}, v_{2}, . . ., v_{n} \in R^{m}$ （向量空间）的集合

$L = a_{1} * v_{1} + a_{2} * v_{2} + . . . + a_{k} * v_{k} : a_{1}, a_{2}, . . ., a_{n} \in Z .$

格L的基，可以是任意一组生成L的线性无关的向量。基的选择不唯一

下图展示了，由两个不同的基向量组 (u1,u2)，(v1,v2) 构成的二维格：

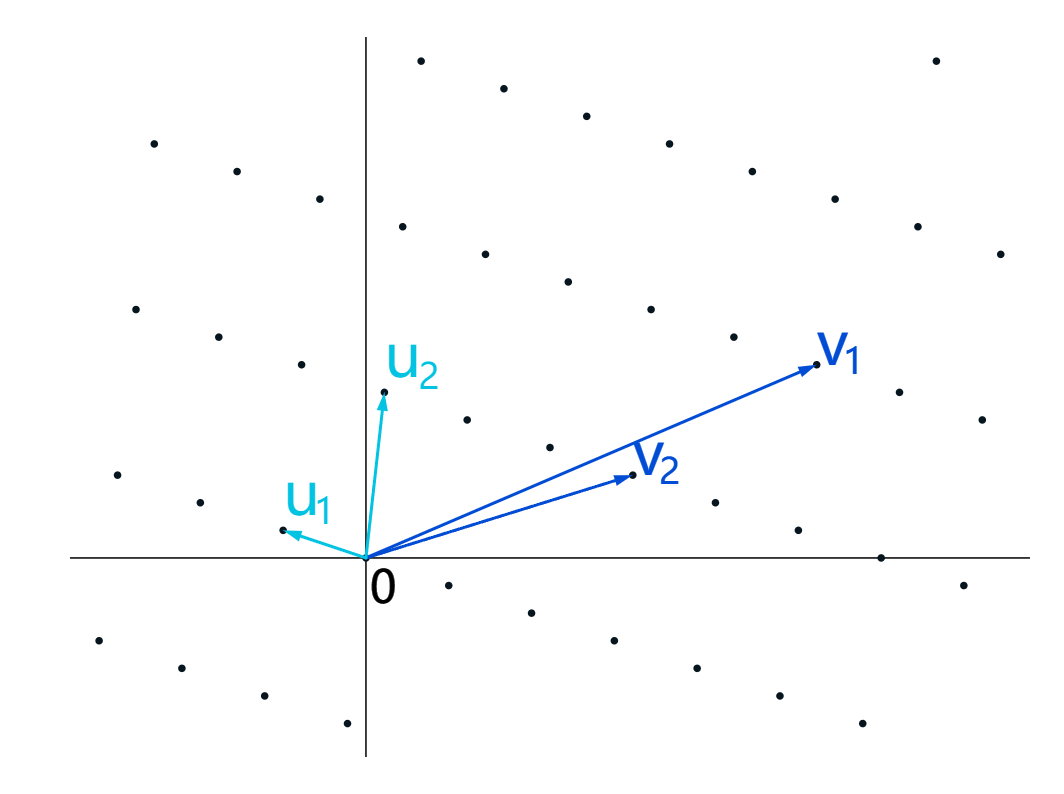
使用基，我们可以用基向量的整数倍到达格 L 内的任何点。基向量还定义了基本域：

$F (v_{1}, . . ., v_{n}) = t_{1} * v_{1} + t_{2} * v_{2} + . . . + t_{n} * v_{n} : 0 \leq t_{i} < 1 .$

计算行列式

行列式（英语：Determinant），记作 $d e t (A)$ 或 $| A |$ 是一个在方块矩阵上计算得到的标量。行列式可以看作是有向面积或体积的概念在一般的欧几里得空间中的推广。

from sage.all import *
v = [[6, 2, -3],[5, 1, 4],[2, 7, 1]]

A = matrix(v)
det(A)

# -255

答案为255

Gaussian Reduction（高斯消元法）

如果你仔细观察，“格”开始出现在密码学中的每一个角落。有时它们操纵一个加密系统，破坏了(生成)不够安全的参数。最著名的例子是 Coppersmith 对 RSA 加密的攻击。

格也可用于构建加密协议，其安全性基于两个基本的“难”问题：

The Shortest Vector Problem (SVP)
给定的基向量和格，找到格 L 中的长度最短非零向量。换言之，找到一个非零向量 $v \in L$ 使 $| | v | |$ 最小

The Closest Vector Problem (CVP)
给定的基向量、格，和一个不在格上的目标向量，找到距离目标向量最近的格向量。给定一个不在格 L 中的向量 $w \in R^{m}$ ，找到向量$ v\in L$ 使 $| | v - w | |$ 最小

对于一般的格，SVP问题十分困难，但对于相对简单的情况，我们有非常有效的算法可以计算出问题的解或者近似解。当格的维数小于等于4时，可以在多项式时间内计算出确定解，对于更高维，只能求出近似解。

高斯发明了一种算法来找到给定任意基的二维格 LLL 的最佳基。算法的输出 v1 是 L 中最短的非零向量，由此解决了二维的SVP问题。

高斯的算法大致通过从另一个基向量中减去一个基向量的倍数来达到目标，直到不再可能使它们变得更小。这适用于二维，因此可以很好地可视化。

题目给了两个向量v = (846835985, 9834798552), u = (87502093, 123094980)，要我们通过应用高斯算法找到最佳基础。flag是新基向量的内积。

使用 sagemath中的 LLL() 算法来计算最优基

from sage.all import *

M = matrix([[846835985, 9834798552],[87502093, 123094980]])
M = M.LLL()
print(M)
v1 = vector([   87502093  , 123094980])
v2 = vector([-4053281223 , 2941479672])

v1*v2	#用于计算内积

out:
[   87502093   123094980]
[-4053281223  2941479672]
7410790865146821

Find the Lattice（寻找格）

https://en.wikipedia.org/wiki/NTRUEncrypt

考察了一个 NTRU 加密系统。

题目：

source.py

from Crypto.Util.number import getPrime, inverse, bytes_to_long
import random
import math

FLAG = b'crypto{?????????????????????}'


def gen_key():
    q = getPrime(512)
    upper_bound = int(math.sqrt(q // 2))
    lower_bound = int(math.sqrt(q // 4))
    f = random.randint(2, upper_bound)
    while True:
        g = random.randint(lower_bound, upper_bound)
        if math.gcd(f, g) == 1:
            break
    h = (inverse(f, q)*g) % q
    return (q, h), (f, g)


def encrypt(q, h, m):
    assert m < int(math.sqrt(q // 2))
    r = random.randint(2, int(math.sqrt(q // 2)))
    e = (r*h + m) % q
    return e


def decrypt(q, h, f, g, e):
    a = (f*e) % q
    m = (a*inverse(f, g)) % g
    return m


public, private = gen_key()
q, h = public
f, g = private

m = bytes_to_long(FLAG)
e = encrypt(q, h, m)

print(f'Public key: {(q,h)}')
print(f'Encrypted Flag: {e}')

output.txt

Public key: (7638232120454925879231554234011842347641017888219021175304217358715878636183252433454896490677496516149889316745664606749499241420160898019203925115292257, 2163268902194560093843693572170199707501787797497998463462129592239973581462651622978282637513865274199374452805292639586264791317439029535926401109074800)
Encrypted Flag: 5605696495253720664142881956908624307570671858477482119657436163663663844731169035682344974286379049123733356009125671924280312532755241162267269123486523

题目分析：

通过上述代码得到已知量：q，h 和密文 e

$h = f^{- 1} * g m o d q$ ， $e = (r * h + m) m o d q$

需要求解的未知量：f 和 g

由 $h = f^{- 1} * g m o d q$ 得： $h * f = g + k * q \Rightarrow h * f - k * q = g$

选定一组向量 (1 , h) ，(0 , q) ，构造线性无关的向量组 $M = [\begin{matrix} 1 & h \\ 0 & q \end{matrix}]$ ，作为格 L 的基。

根据线性关系可以构造格 L： $[\begin{matrix} f & - k \end{matrix}] [\begin{matrix} 1 & h \\ 0 & q \end{matrix}] = [\begin{matrix} f & g \end{matrix}]$

向量（f , g）可以由这组格基向量 M 和整数系数（f , -k）线性组合表示，因此向量（f , g）也在格 L 上。

所以我们可以利用 LLL 算法计算出这个格的最短向量，也就是（f , g）

sage实现exp:

from sage.all import *
import numpy
from gmpy2 import *
from Crypto.Util.number import *

Public_key = (
7638232120454925879231554234011842347641017888219021175304217358715878636183252433454896490677496516149889316745664606749499241420160898019203925115292257,
2163268902194560093843693572170199707501787797497998463462129592239973581462651622978282637513865274199374452805292639586264791317439029535926401109074800)
enc_flag = 5605696495253720664142881956908624307570671858477482119657436163663663844731169035682344974286379049123733356009125671924280312532755241162267269123486523

q = Public_key[0]
h = Public_key[1]

M = matrix([[1,h],[0,q]])
M = M.LLL()
print(M)

def decrypt(q, h, f, g, e):
    a = (f * e) % q
    m = (a * invert(f, g)) % g
    return m
f,g = 47251817614431369468151088301948722761694622606220578981561236563325808178756,43997957885147078115851147456370880089696256470389782348293341937915504254589
print(long_to_bytes(decrypt(q,h,f,g,enc_flag)))

选择第一组输出的结果，得到flag：

b'crypto{Gauss_lattice_attack!}'

Backpack Cryptography（背包密码）

题目：

source.py

import random
from collections import namedtuple
import gmpy2
from Crypto.Util.number import isPrime, bytes_to_long, inverse, long_to_bytes

FLAG = b'crypto{??????????????????????????}'
PrivateKey = namedtuple("PrivateKey", ['b', 'r', 'q'])

def gen_private_key(size):
    s = 10000
    b = []
    for _ in range(size):
        ai = random.randint(s + 1, 2 * s)
        assert ai > sum(b)
        b.append(ai)
        s += ai
    while True:
        q = random.randint(2 * s, 32 * s)
        if isPrime(q):
            break
    r = random.randint(s, q)
    assert q > sum(b)
    assert gmpy2.gcd(q,r) == 1
    return PrivateKey(b, r, q)


def gen_public_key(private_key: PrivateKey):
    a = []
    for x in private_key.b:
        a.append((private_key.r * x) % private_key.q)
    return a


def encrypt(msg, public_key):
    assert len(msg) * 8 <= len(public_key)
    ct = 0
    msg = bytes_to_long(msg)
    for bi in public_key:
        ct += (msg & 1) * bi
        msg >>= 1
    return ct


def decrypt(ct, private_key: PrivateKey):
    ct = inverse(private_key.r, private_key.q) * ct % private_key.q
    msg = 0
    for i in range(len(private_key.b) - 1, -1, -1):
         if ct >= private_key.b[i]:
             msg |= 1 << i
             ct -= private_key.b[i]
    return long_to_bytes(msg)


private_key = gen_private_key(len(FLAG) * 8)
public_key = gen_public_key(private_key)
encrypted = encrypt(FLAG, public_key)
decrypted = decrypt(encrypted, private_key)
assert decrypted == FLAG

print(f'Public key: {public_key}')
print(f'Encrypted Flag: {encrypted}')

output.txt

sage实现exp:

from gmpy2 import *
from Crypto.Util.number import *


def decrypt(q, h, f, g, e):
    a = (f * e) % q
    m = (a * invert(f, g)) % g
    return m


M = ["Public key 的内容"]
S = 45690752833299626276860565848930183308016946786375859806294346622745082512511847698896914843023558560509878243217521

from hashlib import sha256

n = len(M)
L = matrix.zero(n + 1) # 构造n+1 阶0矩阵

for row, x in enumerate(M):
    L[row, row] = 2
    L[row, -1] = x

L[-1, :] = 1
L[-1, -1] = S
res = L.LLL()
print(res) #注意这里反向量才是解，2x_i - 1 = res[i]

msg = ""
print(res[-16])
for i in -res[-16]:
    if int(i)==-1:
        msg += '0'
    if int(i)== 1:
        msg += '1'
print(msg)
print(long_to_bytes(int(str(msg[::-1]),2)))

flag 二进制值需要逆序一下。

BRAINTEASERS PART1(谜题1)

Successive Powers(连续的大幂)

题目：

序列 588, 665, 216, 113, 642, 4, 836, 114, 851, 492, 819, 237 是某个整数 x 的连续幂次模三位的素数 p 的结果。

flag为 crypto{p,x}

分析题目：

设 m = [588, 665, 216, 113, 642, 4, 836, 114, 851, 492, 819, 237]

先计算出素数 p 的全部可能值，p肯定是要比 m 中的最大值更大的：p_list = [851, 853, 857, 859, 863, 877, 881, 883, 887, 907, 911, 919, 929, 937, 941, 947, 953, 967, 971, 977, 983, 991, 997]

由 $m \equiv x^{k} m o d p$ 可知： $m_{i} \equiv x^{k + i} m o d p$

所以 $\frac{m_{i + 1}}{m_{i}} m o d p = \frac{x^{k + i + 1}}{x^{k + i}} m o d p = x$

$m_{i + 1} = m_{i} * x m o d p$

exp：

from gmpy2 import *
from Crypto.Util.number import *

m = [588, 665, 216, 113, 642, 4, 836, 114, 851, 492, 819, 237]
p_list = []

i = 851
while i < 1000:
    p_list.append(int(i))
    i = next_prime(i)

print(p_list)

for p in p_list:
    for x in range(2, 1000):
        for i in range(len(m) - 1):
            if m[i] * x % p != m[i + 1]:
                break
        else:
            print(f"{x=} and {p=}")
            break

crtpto{209,919}

这里我们用到python的一种很酷的写法：

for a in b:
    # something that may or may not break
else:
    # 当没有任何循环迭代,称为中断时运行

Adrien's Signs(Adrien 的标记)

题目：

from random import randint

a = 288260533169915
p = 1007621497415251

FLAG = b'crypto{????????????????????}'


def encrypt_flag(flag):
    ciphertext = []
    plaintext = ''.join([bin(i)[2:].zfill(8) for i in flag])
    for b in plaintext:
        e = randint(1, p)
        n = pow(a, e, p)
        if b == '1':
            ciphertext.append(n)
        else:
            n = -n % p
            ciphertext.append(n)
    return ciphertext


print(encrypt_flag(FLAG))

output.txt

题目分析：

根据下面这段代码我们可以分析相关数据：已知 $a, p$ 的值，且 $a$ 是模 $p$ 的二次剩余。

即： $a^{(p - 1) / 2} \equiv 1 m o d p$

for b in plaintext:
    e = randint(1, p)
    n = pow(a, e, p)
    if b == '1':
        ciphertext.append(n)
    else:
        n = -n % p
        ciphertext.append(n)
return ciphertext

$n \equiv a^{e} m o d p$ ，则 $n^{\frac{p - 1}{2}} \equiv a^{\frac{p - 1}{2} * e} m o d p = 1 m o d p$ ，所以当 n是模 p 的二次剩余时，则 b = 1，否则b=0；

exp:

from Crypto.Util.number import long_to_bytes

a = 288260533169915
p = 1007621497415251

assert p % 4 == 3
assert pow(a, (p - 1) // 2, p) == 1
print("a是模 p 的二次剩余")

n = [67594220461269, 501237540280788, 718316769824518, 296304224247167, 48290626940198, 30829701196032, 521453693392074, 840985324383794, 770420008897119, 745131486581197, 729163531979577, 334563813238599, 289746215495432, 538664937794468, 894085795317163, 983410189487558, 863330928724430, 996272871140947, 352175210511707, 306237700811584, 631393408838583, 589243747914057, 538776819034934, 365364592128161, 454970171810424, 986711310037393, 657756453404881, 388329936724352, 90991447679370, 714742162831112, 62293519842555, 653941126489711, 448552658212336, 970169071154259, 339472870407614, 406225588145372, 205721593331090, 926225022409823, 904451547059845, 789074084078342, 886420071481685, 796827329208633, 433047156347276, 21271315846750, 719248860593631, 534059295222748, 879864647580512, 918055794962142, 635545050939893, 319549343320339, 93008646178282, 926080110625306, 385476640825005, 483740420173050, 866208659796189, 883359067574584, 913405110264883, 898864873510337, 208598541987988, 23412800024088, 911541450703474, 57446699305445, 513296484586451, 180356843554043, 756391301483653, 823695939808936, 452898981558365, 383286682802447, 381394258915860, 385482809649632, 357950424436020, 212891024562585, 906036654538589, 706766032862393, 500658491083279, 134746243085697, 240386541491998, 850341345692155, 826490944132718, 329513332018620, 41046816597282, 396581286424992, 488863267297267, 92023040998362, 529684488438507, 925328511390026, 524897846090435, 413156582909097, 840524616502482, 325719016994120, 402494835113608, 145033960690364, 43932113323388, 683561775499473, 434510534220939, 92584300328516, 763767269974656, 289837041593468, 11468527450938, 628247946152943, 8844724571683, 813851806959975, 72001988637120, 875394575395153, 70667866716476, 75304931994100, 226809172374264, 767059176444181, 45462007920789, 472607315695803, 325973946551448, 64200767729194, 534886246409921, 950408390792175, 492288777130394, 226746605380806, 944479111810431, 776057001143579, 658971626589122, 231918349590349, 699710172246548, 122457405264610, 643115611310737, 999072890586878, 203230862786955, 348112034218733, 240143417330886, 927148962961842, 661569511006072, 190334725550806, 763365444730995, 516228913786395, 846501182194443, 741210200995504, 511935604454925, 687689993302203, 631038090127480, 961606522916414, 138550017953034, 932105540686829, 215285284639233, 772628158955819, 496858298527292, 730971468815108, 896733219370353, 967083685727881, 607660822695530, 650953466617730, 133773994258132, 623283311953090, 436380836970128, 237114930094468, 115451711811481, 674593269112948, 140400921371770, 659335660634071, 536749311958781, 854645598266824, 303305169095255, 91430489108219, 573739385205188, 400604977158702, 728593782212529, 807432219147040, 893541884126828, 183964371201281, 422680633277230, 218817645778789, 313025293025224, 657253930848472, 747562211812373, 83456701182914, 470417289614736, 641146659305859, 468130225316006, 46960547227850, 875638267674897, 662661765336441, 186533085001285, 743250648436106, 451414956181714, 527954145201673, 922589993405001, 242119479617901, 865476357142231, 988987578447349, 430198555146088, 477890180119931, 844464003254807, 503374203275928, 775374254241792, 346653210679737, 789242808338116, 48503976498612, 604300186163323, 475930096252359, 860836853339514, 994513691290102, 591343659366796, 944852018048514, 82396968629164, 152776642436549, 916070996204621, 305574094667054, 981194179562189, 126174175810273, 55636640522694, 44670495393401, 74724541586529, 988608465654705, 870533906709633, 374564052429787, 486493568142979, 469485372072295, 221153171135022, 289713227465073, 952450431038075, 107298466441025, 938262809228861, 253919870663003, 835790485199226, 655456538877798, 595464842927075, 191621819564547]
flag_bin = ""
for i in n:
    if(pow(i,(p - 1) // 2, p) == 1):
        flag_bin += "1"
    else:
        flag_bin += "0"
print(flag_bin)
print(long_to_bytes(int(flag_bin, 2)))

Modular Binomials(模二项式)⭐

题目：获取素数 p,q

N = p*q
c1 = (2*p + 3*q)**e1 mod N
c2 = (5*p + 7*q)**e2 mod N

N = 14905562257842714057932724129575002825405393502650869767115942606408600343380327866258982402447992564988466588305174271674657844352454543958847568190372446723549627752274442789184236490768272313187410077124234699854724907039770193680822495470532218905083459730998003622926152590597710213127952141056029516116785229504645179830037937222022291571738973603920664929150436463632305664687903244972880062028301085749434688159905768052041207513149370212313943117665914802379158613359049957688563885391972151218676545972118494969247440489763431359679770422939441710783575668679693678435669541781490217731619224470152467768073
e1 = 12886657667389660800780796462970504910193928992888518978200029826975978624718627799215564700096007849924866627154987365059524315097631111242449314835868137
e2 = 12110586673991788415780355139635579057920926864887110308343229256046868242179445444897790171351302575188607117081580121488253540215781625598048021161675697
c1 = 14010729418703228234352465883041270611113735889838753433295478495763409056136734155612156934673988344882629541204985909650433819205298939877837314145082403528055884752079219150739849992921393509593620449489882380176216648401057401569934043087087362272303101549800941212057354903559653373299153430753882035233354304783275982332995766778499425529570008008029401325668301144188970480975565215953953985078281395545902102245755862663621187438677596628109967066418993851632543137353041712721919291521767262678140115188735994447949166616101182806820741928292882642234238450207472914232596747755261325098225968268926580993051
c2 = 14386997138637978860748278986945098648507142864584111124202580365103793165811666987664851210230009375267398957979494066880296418013345006977654742303441030008490816239306394492168516278328851513359596253775965916326353050138738183351643338294802012193721879700283088378587949921991198231956871429805847767716137817313612304833733918657887480468724409753522369325138502059408241232155633806496752350562284794715321835226991147547651155287812485862794935695241612676255374480132722940682140395725089329445356434489384831036205387293760789976615210310436732813848937666608611803196199865435145094486231635966885932646519

分析：

N=p*q，二项式展开定理，结果中有 pq的都消掉了

$c 1 = (2 p)^{e 1} + (3 q)^{e 1}$ $m o d$ $N$

$c 2 = (5 p)^{e 2} + (7 q)^{e 2}$ $m o d$ $N$

==>

$c 1^{e 2} = (2 p)^{e 1 e 2} + (3 q)^{e 1 e 2}$ $m o d$ $N$

$c 2^{e 1} = (5 p)^{e 1 e 2} + (7 q)^{e 1 e 2}$ $m o d$ $N$

==>

$c 1^{e 2} * 5^{e 1 e 2} = (10 p)^{e 1 e 2} + (15 q)^{e 1 e 2}$ $m o d$ $N$

$c 2^{e 1} * 2^{e 1 e 2} = (10 p)^{e 1 e 2} + (14 q)^{e 1 e 2}$ $m o d$ $N$

==>

两式相减得到：

$C$ $=$ $c 1^{e 2} * 5^{e 1 e 2} -$ $c 2^{e 1} * 2^{e 1 e 2}$ = $(15^{e 1 e 2} - 14^{e 1 e 2}) * q^{e 1 e 2}$ $m o d$ $N$

所以 $q$ $= g c d (N, C)$

$p = N / q$

exp:

from gmpy2 import gcd

N = 14905562257842714057932724129575002825405393502650869767115942606408600343380327866258982402447992564988466588305174271674657844352454543958847568190372446723549627752274442789184236490768272313187410077124234699854724907039770193680822495470532218905083459730998003622926152590597710213127952141056029516116785229504645179830037937222022291571738973603920664929150436463632305664687903244972880062028301085749434688159905768052041207513149370212313943117665914802379158613359049957688563885391972151218676545972118494969247440489763431359679770422939441710783575668679693678435669541781490217731619224470152467768073
e1 = 12886657667389660800780796462970504910193928992888518978200029826975978624718627799215564700096007849924866627154987365059524315097631111242449314835868137
e2 = 12110586673991788415780355139635579057920926864887110308343229256046868242179445444897790171351302575188607117081580121488253540215781625598048021161675697
c1 = 14010729418703228234352465883041270611113735889838753433295478495763409056136734155612156934673988344882629541204985909650433819205298939877837314145082403528055884752079219150739849992921393509593620449489882380176216648401057401569934043087087362272303101549800941212057354903559653373299153430753882035233354304783275982332995766778499425529570008008029401325668301144188970480975565215953953985078281395545902102245755862663621187438677596628109967066418993851632543137353041712721919291521767262678140115188735994447949166616101182806820741928292882642234238450207472914232596747755261325098225968268926580993051
c2 = 14386997138637978860748278986945098648507142864584111124202580365103793165811666987664851210230009375267398957979494066880296418013345006977654742303441030008490816239306394492168516278328851513359596253775965916326353050138738183351643338294802012193721879700283088378587949921991198231956871429805847767716137817313612304833733918657887480468724409753522369325138502059408241232155633806496752350562284794715321835226991147547651155287812485862794935695241612676255374480132722940682140395725089329445356434489384831036205387293760789976615210310436732813848937666608611803196199865435145094486231635966885932646519

e = e1*e2

q =gcd(N,pow(c2,e1,N)*pow(2,e,N)-pow(c1,e2,N)*pow(5,e,N))
p = N//q
print(p)
print(q)

Broken RSA(损坏的RSA)⭐

题目

n = 27772857409875257529415990911214211975844307184430241451899407838750503024323367895540981606586709985980003435082116995888017731426634845808624796292507989171497629109450825818587383112280639037484593490692935998202437639626747133650990603333094513531505209954273004473567193235535061942991750932725808679249964667090723480397916715320876867803719301313440005075056481203859010490836599717523664197112053206745235908610484907715210436413015546671034478367679465233737115549451849810421017181842615880836253875862101545582922437858358265964489786463923280312860843031914516061327752183283528015684588796400861331354873
e = 16
ct = 11303174761894431146735697569489134747234975144162172162401674567273034831391936916397234068346115459134602443963604063679379285919302225719050193590179240191429612072131629779948379821039610415099784351073443218911356328815458050694493726951231241096695626477586428880220528001269746547018741237131741255022371957489462380305100634600499204435763201371188769446054925748151987175656677342779043435047048130599123081581036362712208692748034620245590448762406543804069935873123161582756799517226666835316588896306926659321054276507714414876684738121421124177324568084533020088172040422767194971217814466953837590498718

由加密公式 $c \equiv m^{e} m o d n$ 得到 $c t \equiv m^{16} m o d n$ ，我们直接用sage 构造模n下的多项式环，然后计算多项式 $m^{16} - c t$ 在模n下的所有根

这里采用的是多项式的根查找方法是通过寻找多项式方程 $f (x) = 0$ ,解 $x$ 的方法。

**注：**对于多项式方程的计算，采用多项式的根查找方法要比直接使用有限域上的开根函数 nth_root()速度更快

exp:

from sage.all import PolynomialRing
from Crypto.Util.number import long_to_bytes
n = 27772857409875257529415990911214211975844307184430241451899407838750503024323367895540981606586709985980003435082116995888017731426634845808624796292507989171497629109450825818587383112280639037484593490692935998202437639626747133650990603333094513531505209954273004473567193235535061942991750932725808679249964667090723480397916715320876867803719301313440005075056481203859010490836599717523664197112053206745235908610484907715210436413015546671034478367679465233737115549451849810421017181842615880836253875862101545582922437858358265964489786463923280312860843031914516061327752183283528015684588796400861331354873
e = 16
ct = 11303174761894431146735697569489134747234975144162172162401674567273034831391936916397234068346115459134602443963604063679379285919302225719050193590179240191429612072131629779948379821039610415099784351073443218911356328815458050694493726951231241096695626477586428880220528001269746547018741237131741255022371957489462380305100634600499204435763201371188769446054925748151987175656677342779043435047048130599123081581036362712208692748034620245590448762406543804069935873123161582756799517226666835316588896306926659321054276507714414876684738121421124177324568084533020088172040422767194971217814466953837590498718

R.<x> = Zmod(n)[] #定义模n下的多项式环
f = x^16 - ct
m = f.roots()

for i in m:
    flag = long_to_bytes(int(i[0]))
    if b"crypto{" in flag:
        print(flag)

b"Hey, if you are reading this maybe I didn't mess up my code too much. Phew. I really should play more CryptoHack before rushing to code stuff from scratch again. Here's the flag: crypto{m0dul4r_squ4r3_r00t}"

No Way Back Home(无路可归)⭐

题目:

from Crypto.Cipher import AES
from Crypto.Util.Padding import pad, unpad
from hashlib import sha256
from Crypto.Util.number import getPrime, GCD, bytes_to_long, long_to_bytes, inverse
from random import randint

FLAG = b'crypto{????????????????????????????????}'

p, q = getPrime(512), getPrime(512)
n = p * q

# Alice side
v = (p * randint(1, n)) % n
k_A = randint(1, n)
while GCD(k_A, n) != 1:
    k_A = randint(1, n)
vka = (v * k_A) % n

# Bob side
k_B = randint(1, n)
while GCD(k_B, n) != 1:
    k_B = randint(1, n)
vkakb = (vka * k_B) % n

# Alice side
vkb = (vkakb * inverse(k_A, n)) % n

# Bob side
v_s = (vkb * inverse(k_B, n)) % n

# Alice side
key = sha256(long_to_bytes(v)).digest()
cipher = AES.new(key, AES.MODE_ECB)
m = pad(FLAG, 16)
c = cipher.encrypt(m).hex()

out = ""
out += f"p, q = ({p}, {q}) \n"
out += f"vka = {vka} \n"
out += f"vkakb = {vkakb} \n"
out += f"vkb = {vkb} \n"
out += f"c = '{c}' \n"
with open("out.txt", "w") as f:
    f.write(out)

out.txt

题目分析：

核心加密代码为下： $v k a, v k a k b, v k b, p, q$ 为已知量，我们需要计算出 $v$ 的值然后解 AES即可。

p, q = getPrime(512), getPrime(512)
n = p * q
v = (p * randint(1, n)) % n

k_A = randint(1, n)
vka = (v * k_A) % n

k_B = randint(1, n)
vkakb = (vka * k_B) % n

vkb = (vkakb * inverse(k_A, n)) % n

$n = p * q$ ， $v = p * r$ （ $r$ 为随机值）

$v k a \equiv v * k A (m o d n) = p * r * k A (m o d n)$

$v k a k b \equiv v k a * k B (m o d n) = p * r * k A * k B (m o d n)$

$v k b \equiv v k a k b * (k A)^{- 1} (m o d n) = p * r * k B (m o d n)$

可以看出 $v * v k a k b = v k a * v k b$ ，所以等式左右同乘一个 $(v k a k b)^{- 1}$ 逆元，即可得到 $v$ 的值。

但是因为 $g c d (v k a k b, n) = p \neq 1$ ，所以 $v k a k b$ 不存在逆元，使得 $v k a k b * (v k a k b)^{- 1} \equiv 1 m o d n$ 。

我们对上面的同余式进行一个整除 p 的操作，这样使得 $g c d (v k a k b / / p, n) = 1$

$v = (v k a / / p) * (v k b / / p) * p o w (v k a k b / / p, - 1, q) * p = (r * k A m o d q) * (r * k B m o d q) * ((r * k A * k B)^{- 1} m o d q) * p = r * p m o d q$

与加密代码中的 v = (p * randint(1, n)) % n 一致，用一般同余组的思想进行拆分可以得到：

v = (p * randint(1, n)) % q

实现EXP:

from gmpy2 import *
from Crypto.Cipher import AES
from hashlib import sha256
from Crypto.Util.number import *

p, q = (
    10699940648196411028170713430726559470427113689721202803392638457920771439452897032229838317321639599506283870585924807089941510579727013041135771337631951,
    11956676387836512151480744979869173960415735990945471431153245263360714040288733895951317727355037104240049869019766679351362643879028085294045007143623763)
vkb = 6568897840127713147382345832798645667110237168011335640630440006583923102503659273104899584827637961921428677335180620421654712000512310008036693022785945317428066257236409339677041133038317088022368203160674699948914222030034711433252914821805540365972835274052062305301998463475108156010447054013166491083
vka = 124641741967121300068241280971408306625050636261192655845274494695382484894973990899018981438824398885984003880665335336872849819983045790478166909381968949910717906136475842568208640203811766079825364974168541198988879036997489130022151352858776555178444457677074095521488219905950926757695656018450299948207
vkakb = 114778245184091677576134046724609868204771151111446457870524843414356897479473739627212552495413311985409829523700919603502616667323311977056345059189257932050632105761365449853358722065048852091755612586569454771946427631498462394616623706064561443106503673008210435922340001958432623802886222040403262923652
c = 'fef29e5ff72f28160027959474fc462e2a9e0b2d84b1508f7bd0e270bc98fac942e1402aa12db6e6a36fb380e7b53323'
n = p * q
v = ((vka // p) % q * (vkb // p) % q * invert(vkakb // p, q)) % q * p
# 写法二：
# v = vka * vkb * invert(vkakb, q) % n     

key = sha256(long_to_bytes(v)).digest()
cipher = AES.new(key, AES.MODE_ECB)
c = bytes.fromhex(c)
m = cipher.decrypt(c)
print(m)

BRAINTEASERS PART(谜题2)⭐

Ellipse Curve Cryptography(椭圆曲线加密)

这里涉及到椭圆曲线密码学中的一类特殊曲线，亏格为0的曲线 $x^{2} - D y^{2} = 1$ ，这里也可看作是 $G F (p)$ 上的pell方程。

映射公式为： $ϕ : (x, y) ⟼ x - \sqrt{D} y$

注

相关知识点文章：1. 曲线 $x 2 - D y 2 = 1$

题目分析： 这个题目考的是曲线上的 Diffie_Hellman 算法，求解曲线上的 DLP 问题。然后计算出AB的共享密钥，再解AES即可。

已知量为：A，B的公钥信息和AES的密钥及密文信息，曲线的基点G和有限域 p的值。

assert (A.x**2 - D*A.y**2) % p == 1
assert (B.x**2 - D*B.y**2) % p == 1

通过断言语句可以得知使用的曲线形式。利用上面的映射公式可以将曲线上的DLP问题简化为有限域 $F_{p}$ 上的DLP问题。

sagemath实现EXP:

import hashlib
from collections import namedtuple
from Crypto.Cipher import AES
from sage.all import *
from gmpy2 import *


def point_addition(P, Q):
    Rx = (P.x * Q.x + D * P.y * Q.y) % p
    Ry = (P.x * Q.y + P.y * Q.x) % p
    return Point(Rx, Ry)


def scalar_multiplication(P, n):
    Q = Point(1, 0)
    while n > 0:
        if n % 2 == 1:
            Q = point_addition(Q, P)
        P = point_addition(P, P)
        n = n // 2
    return Q


def decrypt_flag(shared_secret: int, iv: str, encrypted: str):
    sha1 = hashlib.sha1()
    sha1.update(str(shared_secret).encode('ascii'))
    key = sha1.digest()[:16]
    # decrypt flag
    iv = bytes.fromhex(iv)
    decrypted = bytes.fromhex(encrypted)

    cipher = AES.new(key, AES.MODE_CBC, iv)
    plaintext = cipher.decrypt(decrypted)
    return plaintext


Point = namedtuple("Point", "x y")
D = 529
sqrt_D = int(iroot(D, 2)[0])  # 23
assert iroot(D, 2)[1] == True  # 能正确开根

p = 173754216895752892448109692432341061254596347285717132408796456167143559
G = Point(29394812077144852405795385333766317269085018265469771684226884125940148,
          94108086667844986046802106544375316173742538919949485639896613738390948)
A = Point(155781055760279718382374741001148850818103179141959728567110540865590463,
          73794785561346677848810778233901832813072697504335306937799336126503714)
B = Point(171226959585314864221294077932510094779925634276949970785138593200069419,
          54353971839516652938533335476115503436865545966356461292708042305317630)

# 注意 sqrt_D是有限域 GF(p) 上的
g = G.x - GF(p)(sqrt_D) * G.y
A = A.x - GF(p)(sqrt_D) * A.y
print(g)
# A的私钥
n_a = discrete_log(A, g)
print(n_a)

S = scalar_multiplication(B, n_a)
print(S)

# decrypt flag
cipher = {'iv': '64bc75c8b38017e1397c46f85d4e332b',
          'encrypted_flag': '13e4d200708b786d8f7c3bd2dc5de0201f0d7879192e6603d7c5d6b963e1df2943e3ff75f7fda9c30a92171bbbc5acbf'}
iv = cipher["iv"]
c = cipher["encrypted_flag"]
shared_secret = S.x

print(decrypt_flag(shared_secret, iv, c))

Roll your Own(自己动手)

根据题目要求输入的 (g,n) 需要满足：pow(g,q,n) = 1

我们设 $n = q^{2}$ ， $g = q + 1$ ，那么由二项式展开定理可得： $(q + 1)^{q} m o d q^{2} = 1$

题目给的密文为： $h \equiv g^{x} m o d n$ ，需要我们求解 x

有： $h = (q + 1)^{x} \equiv q x + 1 m o d q^{2}$

所以 $x = (h - 1) / / q$

EXP:

from pwn import *
import json

r = remote("socket.cryptohack.org", 13403)
r.recvuntil(b"Prime generated:")
p = int(r.recvline().strip().decode("utf-8")[1:-1], 16)
print("p =",p)
r.recvuntil(b"Send integers (g,n) such that pow(g,q,n) = 1: ")

payload = {"g": hex(p + 1), "n": hex(p ** 2)}
r.sendline(json.dumps(payload).encode())
r.recvuntil(b"Generated my public key: ")
h = int(r.recvline().strip().decode("utf8")[1:-1], 16)
print("h =",h)
r.recvuntil(b"What is my private key: ")
r.sendline(json.dumps({"x": hex((h-1)//p)}).encode())

r.recvline()

Unencryptable(不可加密)

题目：

source.py

output.txt

根据题目给出的信息有：

$D A T A^{e} \equiv D A T A m o d N$

$c \equiv m^{e} m o d N$ ， $N = p * q$

我们令 DATA = k，则有： $k^{e} - k \equiv 0 m o d N$ ，即 $N | (k^{e - 1} - 1) * k$

$e - 1 = 2^{16}$ ，所以 $N | (k^{2^{16}} - 1)$ ，所以 $k^{2^{16}} - 1$ 的范围值中应该存在公因数 p 或者 q

考察的： RSA Fixed Points and Shor's Algorithm.

exp：

from Crypto.Util.number import getPrime, inverse, bytes_to_long, long_to_bytes
from gmpy2 import gcd

DATA = bytes.fromhex("372f0e88f6f7189da7c06ed49e87e0664b988ecbee583586dfd1c6af99bf20345ae7442012c6807b3493d8936f5b48e553f614754deb3da6230fa1e16a8d5953a94c886699fc2bf409556264d5dced76a1780a90fd22f3701fdbcb183ddab4046affdc4dc6379090f79f4cd50673b24d0b08458cdbe509d60a4ad88a7b4e2921")

N = 0x7fe8cafec59886e9318830f33747cafd200588406e7c42741859e15994ab62410438991ab5d9fc94f386219e3c27d6ffc73754f791e7b2c565611f8fe5054dd132b8c4f3eadcf1180cd8f2a3cc756b06996f2d5b67c390adcba9d444697b13d12b2badfc3c7d5459df16a047ca25f4d18570cd6fa727aed46394576cfdb56b41
e = 0x10001
c = 0x5233da71cc1dc1c5f21039f51eb51c80657e1af217d563aa25a8104a4e84a42379040ecdfdd5afa191156ccb40b6f188f4ad96c58922428c4c0bc17fd5384456853e139afde40c3f95988879629297f48d0efa6b335716a4c24bfee36f714d34a4e810a9689e93a0af8502528844ae578100b0188a2790518c695c095c9d677b

m = bytes_to_long(DATA)
for i in range(16):
    p = gcd(pow(m,2**i) - 1,N)
    q = N//p
    if p != 1 and p != N and p*q == N:
        print("p =",p)
        phi = (p-1)*(q-1)
        d = inverse(e,phi)
        m = pow(c,d,N)
        print(long_to_bytes(m))

https://hackmd.io/@DSAteam/SyERaIzlC#Primes

exp：

from Crypto.Util.number import *
import itertools
from tqdm import tqdm

def generate_basis(n):
    basis = [True] * n
    for i in range(3, int(n**0.5)+1, 2):
        if basis[i]:
            basis[i*i::2*i] = [False]*((n-i*i-1)//(2*i)+1)
    return [2] + [i for i in range(3, n, 2) if basis[i]]


def miller_rabin(n, b):
    """
    Miller Rabin test testing over all
    prime basis < b
    """
    basis = generate_basis(b)
    if n == 2 or n == 3:
        return True

    if n % 2 == 0:
        return False

    r, s = 0, n - 1
    while s % 2 == 0:
        r += 1
        s //= 2
    for b in basis:
        x = pow(b, s, n)
        if x == 1 or x == n - 1:
            continue
        for _ in range(r - 1):
            x = pow(x, 2, n)
            if x == n - 1:
                break
        else:
            return False
    return True



def xgcd(a, b):
    s = 0
    t = 1
    r = b
    s1 = 1
    t1 = 0
    r1 = a
    while not (r == 0):
        q = r1//r
        r1, r = r, r1-q*r
        s1, s = s, s1-q*s
        t1, t = t, t1-q*t
        #print(r1, s1, t1)
    return (r1, s1, t1)

def crt1(residues, modulos):
    #print(modulos)
    rm = list(zip(residues, modulos))
    cur_res, cur_mod = rm[0]
    for r, m in rm[1:]:
        
        g = GCD(cur_mod, m)
        
        if not r % g == cur_res % g:
            return -1, -1
        r1, s, t = xgcd(m//g, cur_mod//g)
       # print(r, cur_res, r % g, cur_res%g, s, t)
        cur_res = cur_res * m//g * s + r * cur_mod//g * t
        cur_mod *= m//g
        cur_res %= cur_mod
    return cur_res, cur_mod

primes = generate_basis(64)
print(len(primes))
fool = []
h = 3
def legendre(a, p):
    # if a == 2:
        # return (-1)**((p**2-1)//8)
    return pow(a, (p-1)//2, p)

for p in primes:
    f = set()
    for i in generate_basis(200*p)[1:]:
        #print(legendre(p, i))
        if legendre(p, i) == i-1:
            f.add(i % (4*p))
            
    fool.append(list(f))
    
print(primes)
#print(fool)
ks = [1, 998244353, 233]   
fool2 = []
for p, f in enumerate(fool):
    prime = primes[p]
    m = prime*4
    cur_set = set(f)
    for i in range (1, h):
        new_set = set()
        for ff in f:
            if ((ff + ks[i] - 1)*inverse(ks[i], m)) % 4 == 3:
                new_set.add(((ff + ks[i] - 1)*inverse(ks[i], m)) % m)
        cur_set = cur_set.intersection(new_set)
    fool2.append(cur_set)
print(fool2)
mm = 1
for a in fool2:
    mm *= len(a)

print(mm)
pr = 0
for tup in itertools.product(*fool2):
    residues = []
    modulos = []
    #modul = 1
    for i, t in enumerate(tup):
        residues.append(t)
        modulos.append(primes[i]*4)
        # g = GCD(primes[i]*4, modul)
        # modul *= (primes[i]*4)//g
    residues.append(ks[1]-inverse(ks[2], ks[1]))
    modulos.append(ks[1])
    residues.append(ks[2]-inverse(ks[1], ks[2]))    
    modulos.append(ks[2])
    #print(modulos)

    sol, modul = crt1(residues, modulos)
    #rint(sol)
    #print(modul)
    #print(sol)
    found = False
    if not sol == -1:
        cur_t = sol
        #print(sol % modul)
        cur_t = 2**73*modul + cur_t
        for i in tqdm(range(100000)):
            if isPrime(cur_t):
                fin = cur_t
                facs = [cur_t]
                for ii in range(1, h):
                    facs.append(ks[ii]*(cur_t-1) + 1)
                    fin *= ks[ii]*(cur_t-1) + 1
                #print(fin.bit_length())
                if(miller_rabin(fin, 64)):
                    print(isPrime(fin))
                    print(fin)
                    print(facs)
                    if fin.bit_length() >= 600 and fin.bit_length() <= 900:
                        found = True
                        break
            cur_t += modul

    if found:
        break

用 json 格式进行交互即可。

MatheMatics(数学)

MODULAR MATH(模块化数学)

Quadratic Residues(二次剩余)

Legendre Symbol(勒让德符号)

Modular Square Root(模平方根)

Chinese Remainder Theorem(中国剩余定理)

LATTICES(格)

Vectors(向量)

Size and Basis(大小和基)

Gram Schmidt(施密特正交化)

What's a Lattice?（什么是格子）

Gaussian Reduction（高斯消元法）

Find the Lattice（寻找格）

Backpack Cryptography（背包密码）

BRAINTEASERS PART1(谜题1)

Successive Powers(连续的大幂)

Adrien's Signs(Adrien 的标记)

Modular Binomials(模二项式)⭐

Broken RSA(损坏的RSA)⭐

No Way Back Home(无路可归)⭐

BRAINTEASERS PART(谜题2)⭐

Ellipse Curve Cryptography(椭圆曲线加密)

Roll your Own(自己动手)

Unencryptable(不可加密)

Cofactor Cofantasy(辅助因子Cofantasy)

Real Eisenstein(真正的艾森斯坦)

PRIMES(素数)

Prime and Prejudice(最初与偏见)